IIR-Filter
Introduction¶
An IIR filter has an impulse response that lasts for infinite duration, meaning it does not reaches zero. It has a feedback loop. IIR filters are recursive (1) in nature. They can achieve a specified frequency response using fewer coefficients/taps (due to presence of feedback) than FIR filters.
- Recursive filters are the filters where the output depends on current and past inputs and output values. Since, there is a feedback present in IIR filter, it is a recursive filters. Example of non-recursive filters are FIR filters where output does not depend on past outputs.
Fig 1: Logical structure of IIR filter (Direct form 1). Block z-1 represent delay using z-transforms.
The filter shown above can be mathematically represented as follows :
$$y(n)=b_0x(n)+b_1x(n-1)+\dots{}+b_Mx(n-M)-a_1y(n-1)-+\dots{}-a_Ny(n-N)$$
$$=\sum_{i=0}^{M}b_ix(n-i)-\sum_{j=1}^{N}a_jy(n-j)$$
An IIR filter (as shown above) has both forward path (\(b_0,b_1,b_2\)) and feedback path (\(a_1,a_2\)). This means it has both poles and zeros. So for an IIR filter, stability has to be analysed. Unlike FIR filters, IIR filters generally have a non-linear phase, meaning different frequencies are delayed by different amounts.
Figure 1 represents a structure called Direct form 1. The number of delay blocks can be reduced to half in Direct form 2 shown below.
Another way of representing IIR filter is called lattice ladder structure.
Number of Taps¶
Taps refers to the filter's coefficients that determine its frequency response. Unlike finite impulse response (FIR) filters, IIR filters use fewer taps to achieve a desired response because of presence of feedback in IIR filters.
IIR filters can achieve a frequency response that would require many more taps in a FIR filter, making IIR filter more computationally efficient.
z-transform of an IIR filter¶
$$y(n)=b_0x(n)+b_1x(n-1)+\dots{}+b_Mx(n-M)-a_1y(n-1)-+\dots{}-a_Ny(n-N)$$
$$y(z)=b_0x(z)+b_1x(z)z^{-1}+\dots{}+b_Mx(z)z^{-M}-a_1y(z)z^{-1}-a_2y(z)z^{-2}-\dots{}-a_Ny(z)z^{-N}$$
$$\cfrac{y(z)}{x(z)}=H(z)=\cfrac{b_0+b_1z^{-1}+\dots{}+b_Mz^{-M}}{1+a_1z^{-1}+a_2z^{-2}+\dots{}a_Nz^{-N}}$$
The z-transform of IIR filter shows that the denominator is a polynomial. Therefore, it has poles.
Types of IIR filter¶
On the basis of filtering characteristics¶
On the basis of coefficients¶
- Butterworth
- Chebyshev
- Elliptic
- Bessel
Applications¶
IIR filters are used in applications where memory is limited and linear phase is not critical.
IIR filter using MATLAB¶
n = 5;
[z,p,k] = buttap(n);
[bBp,aBp] = zp2tf(z,p,k);
[hBp,wBp] = freqs(bBp,aBp,4096);
semilogx(wBp,abs(hBp))
grid on
xlabel("Frequency (rad/s)")
ylabel("Magnitude")
Examples¶
Transfer function analysis¶
$$H(z)=\cfrac{0.75z^{-2}+z^{-1}-1}{1-2z^{-1}}$$ The above function represents a IIR system because denominator is not a constant instead it is a polynomial in \(z^{-1}\). It has zeros located at -1/2 and 3/2. Poles at 0 and 2.
Spectrum of H(z)¶
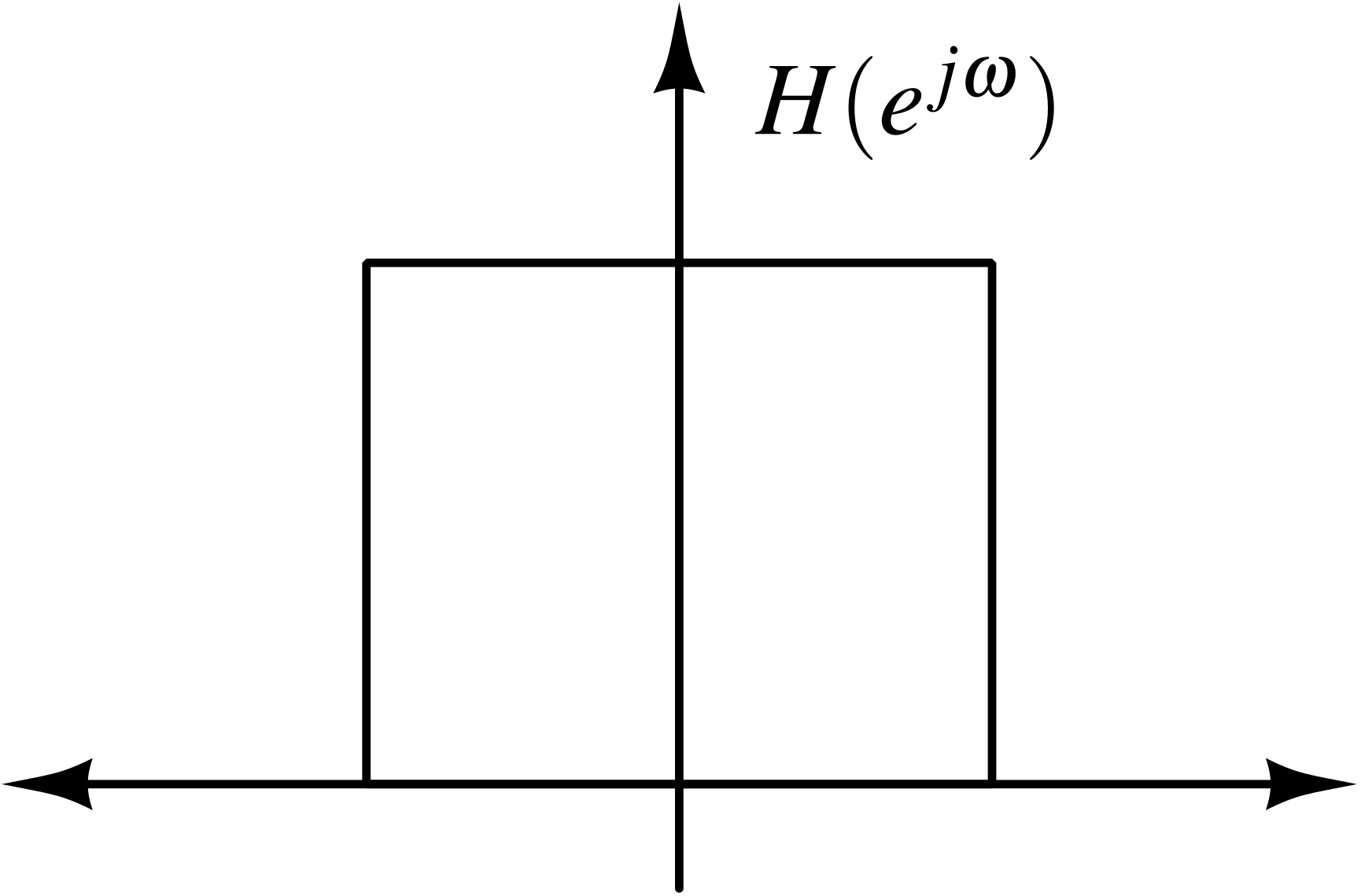The above system represents an IIR system. Because \(H(e^{j\omega{}})\) is finite in frequency domain \([-\pi,\pi]\). Meaning, \(h[n]\) must be infinite in time domain. Therefore, \(h[n]\) has an infinite impulse response.