Initial Value Theorem

Introduction¶

In Control Theory and Laplace transform, the initial value theorem helps to find the time domain value of function $x(t)$ at time t=0 (initial time) without needing to find the inverse Laplace transform $\mathcal{L}^{-1}[X(s)]$. Finding inverse Laplace transform could be complicated and time consuming.

Initial Value of a signal

Definition¶

Initial value theorem of Laplace transform states that,

$$x(t)\leftrightarrow{}X(s)$$

Then,

$$\lim_{t\rightarrow{}0}x(t)=x(0)=\lim_{s\rightarrow{}\infty}sX(s)$$

For z-transforms, if

$$x[n]\leftrightarrow{}X(z)$$

Then,

$$x[0]=\lim_{z\rightarrow{}\infty{}}X(z)$$

Example of Initial Value theorem¶

Find the initial time domain value of function :

$$X(s)=\cfrac{1}{s}+\cfrac{1}{s^2+2s+2}+\cfrac{s+1}{s^2+2s+2}$$

Multiply the transfer function $X(s)$ by $s$.
Take the limit of $sX(s)$ as $s\rightarrow{}\infty{}$
Result is value of $x(t)$ when $t=0$.

$$\lim_{s\rightarrow{}\infty{}}s\left(\cfrac{1}{s}+\cfrac{1}{s^2+2s+2}+\cfrac{s+1}{s^2+2s+2}\right)=2$$

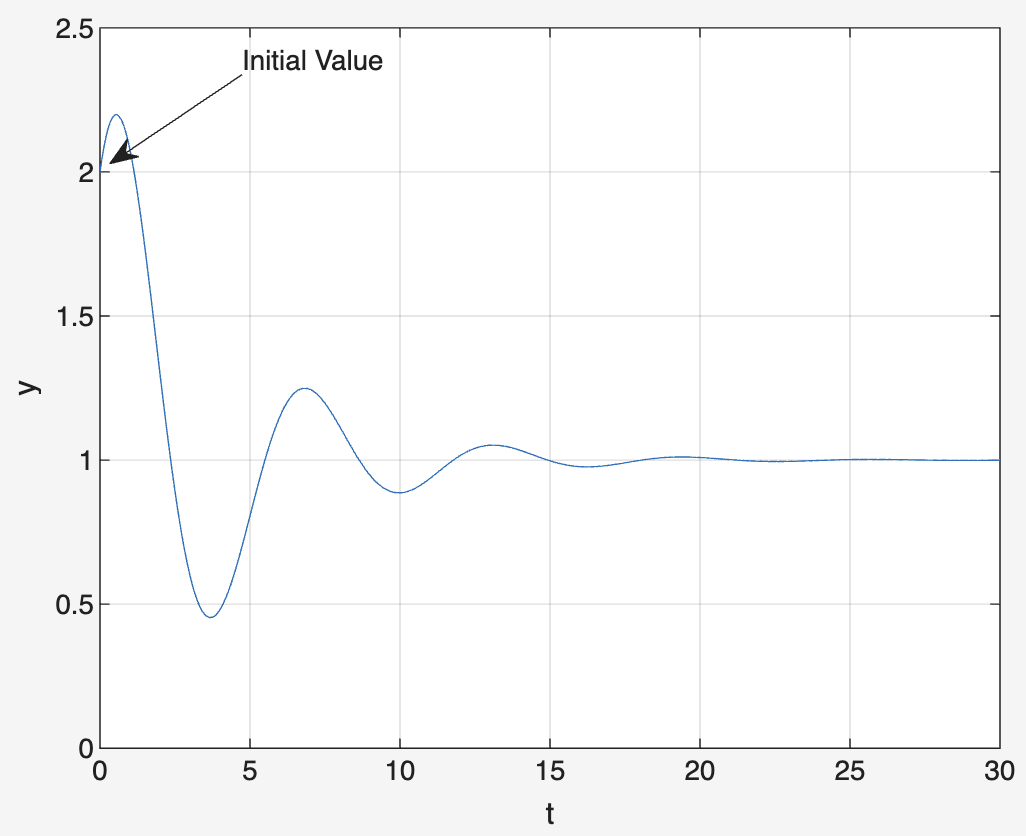
The initial time domain value is 2.

Inverse Laplace Transform method

Using partial fractions we can find the inverse laplace transform of the above function. We get, $$x(t)=1+e^{-t}[\sin(t)+\cos(t)]$$ If we substitute $t=0$, we get $x(0)=2$ which matches initial value theorem.

Derivation of Initial value theorem for Laplace transform¶

Laplace transform of signal $x(t)u(t)$ is :

$$\mathcal{L}[x(t)]=X(s)=\int_{0}^{\infty}x(t)e^{-st}dt$$

Taking derivative of both sides :

$$\mathcal{L}[\cfrac{dx(t)}{dt}]=\int_{0}^{\infty}\cfrac{dx(t)}{dt}e^{-st}dt$$

Using derivative in time-domain property of Laplace transform,

$$\mathcal{L}[\cfrac{dx(t)}{dt}]=\int_{0}^{\infty}\cfrac{dx(t)}{dt}e^{-st}dt=sX(s)-x(0)$$

$$\implies{}\lim_{s\rightarrow{}\infty{}}\int_{0}^{\infty}\cfrac{dx(t)}{dt}e^{-st}dt=\lim_{s\rightarrow{}\infty{}}\left(sX(s)-x(0)\right)$$

$$\implies{}0=\lim_{s\rightarrow{}\infty{}}\left(sX(s)-x(0)\right)$$

$$\implies{}x(0)=\lim_{s\rightarrow{}\infty{}}sX(s)$$