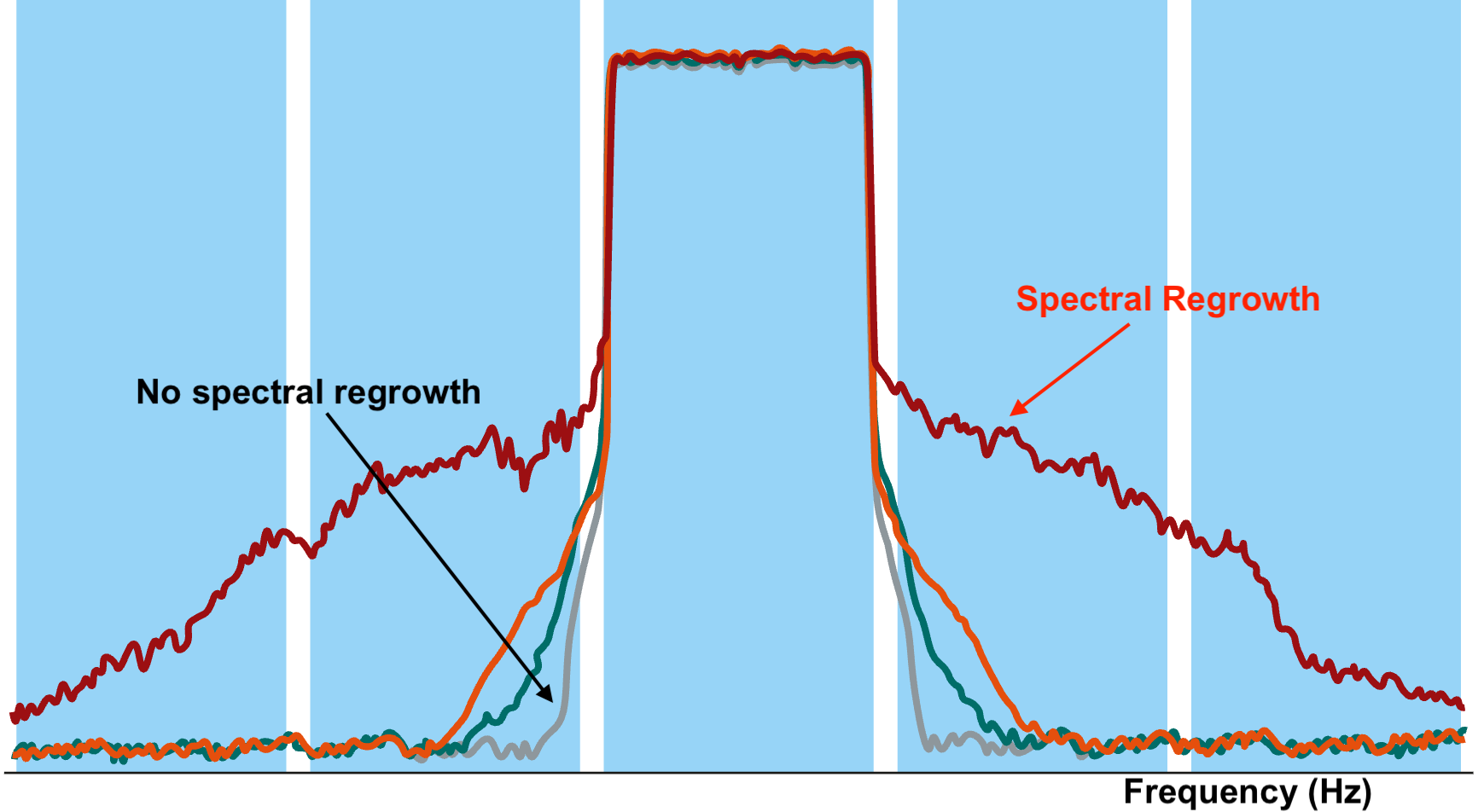
Spectral Regrowth¶
Spectral regrowth is the unwanted generation of new frequency components (intermodulation products) around a main carrier signal, caused by nonlinearities and phase noise of the components in the signal chain.
Nonlinearity in signal chain can cause spectral regrowth. One such source of non-linearity is linear power-amplifier. Variable-amplitude schemes like 16-QAM, QPSK and ASK, are distorted by power-amplifier's compression.
A modulated waveform x(t)=A(t)cos[ωct+φ(t)] is said to have a constant envelope if A(t) does not vary with time. Constant and variable-envelope signals behave differently in a nonlinear system.
Constant envelope signal through a PA¶
Suppose the power amplifier is represented by following model:
$$y(t)=\alpha{}_1x(t)+\alpha{}_3x^3(t)+\dots{}$$
Substituting x(t)=Accos[ωct+φ(t)] :
$$y(t)=\alpha{}_1A_c\cos[\omega{}_ct+\phi{}(t)]+\alpha{}_3A_c^3\cos^3[\omega{}_ct+\phi{}(t)]+\dots{}$$
$$y(t)=\alpha{}_1A_c\cos[\omega{}_ct+\phi{}(t)]+\cfrac{\alpha{}_3A_c^3}{4}\cos[3\omega{}_ct+3\phi{}(t)]+\cfrac{3\alpha{}_3A_c^3}{4}\cos[\omega{}_ct+\phi{}(t)]+\dots{}$$
The second-term above represents a modulated signal around ω=3ωc. Since the bandwidth of the original signal, Accos[ωct+φ], is typically much less than ωc, the bandwidth occupied by cos[3ωct+φ] is small enough that it does not reach the fundamental frequency of ωc. Thus, the shape of the spectrum in the vicinity of ωc remains unchanged.
Variable envelope signal through a PA¶
Now consider a variable-envelope signal (QPSK) applied to the above nonlinear system. We can model in the input signal, x(t) as:
$$x(t)=A(t)\cos(\omega{}_ct)$$
where A(t) represents the time varying envelope of the signal. We have :
$$y(t)=\alpha{}_1[A(t)\cos(\omega{}_ct)]+\alpha{}_3\left[A(t)\cos(\omega{}_ct)\right]^3+\dots{}$$
$$y(t)=[\alpha{}_1A(t)+\underbrace{(3/4)\alpha{}_3A^3(t)}_{\text{spectral regrowth}}]\cos(\omega{}_ct)+\cfrac{\alpha{}_3A^3(t)}{4}\cos(3\omega{}_ct)+\dots{}$$
Thus, the output contains the spectra of A3(t) centered around ωc. A3(t) exhibits a broader spectrum than A(t), we say the spectrum “grows” when a variable-envelope signal passes through a nonlinear system.
Variable vs Constant envelope signals
It can be noted from above discussions that variable envelope signals causes spectral regrowth.
Adjacent channel power ratio (ACPR)¶
ACPR measures the total system interference and distortion performance. Spectral regrowth increases ACPR. ACPR is a system measurement and is generally defined as the ratio of the average power in the adjacent frequency channel to the average power in the transmitted frequency channel (wanted or modulated signal). It is analogous to the third-order intercept point (OIP3) metric commonly used to characterize the linearity performance of RF devices. It is a critical measurement for CDMA and WCDMA transmitters and their components. In 3GPP-WCDMA systems, ACPR is referred to as the adjacent-channel leakage ratio (ACLR).
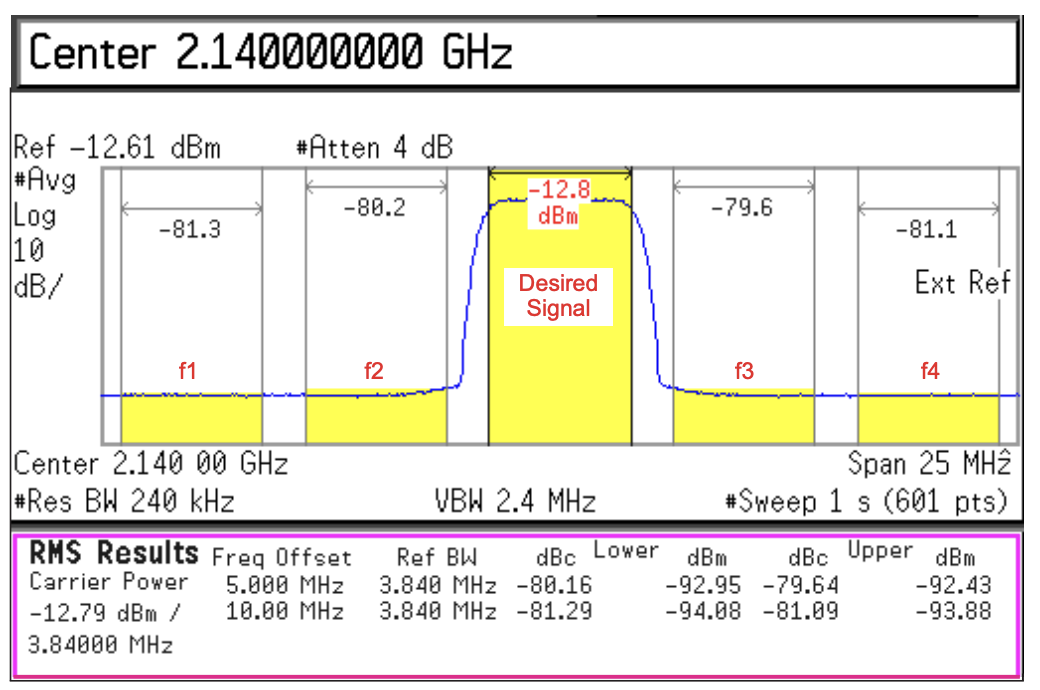
The figure above illustrates the power spectrum of a single-carrier WCDMA signal along with the adjacent-channel power arising from third-order intermodulation products. In this example, the carrier power is −12.8 dBm. The power levels in the two adjacent channels are −79.6 dBc (upper, f3) and −80.2 dBc (lower, f2). The alternate channel powers are −81.1 dBc (f4) and −81.3 dBc (f1).
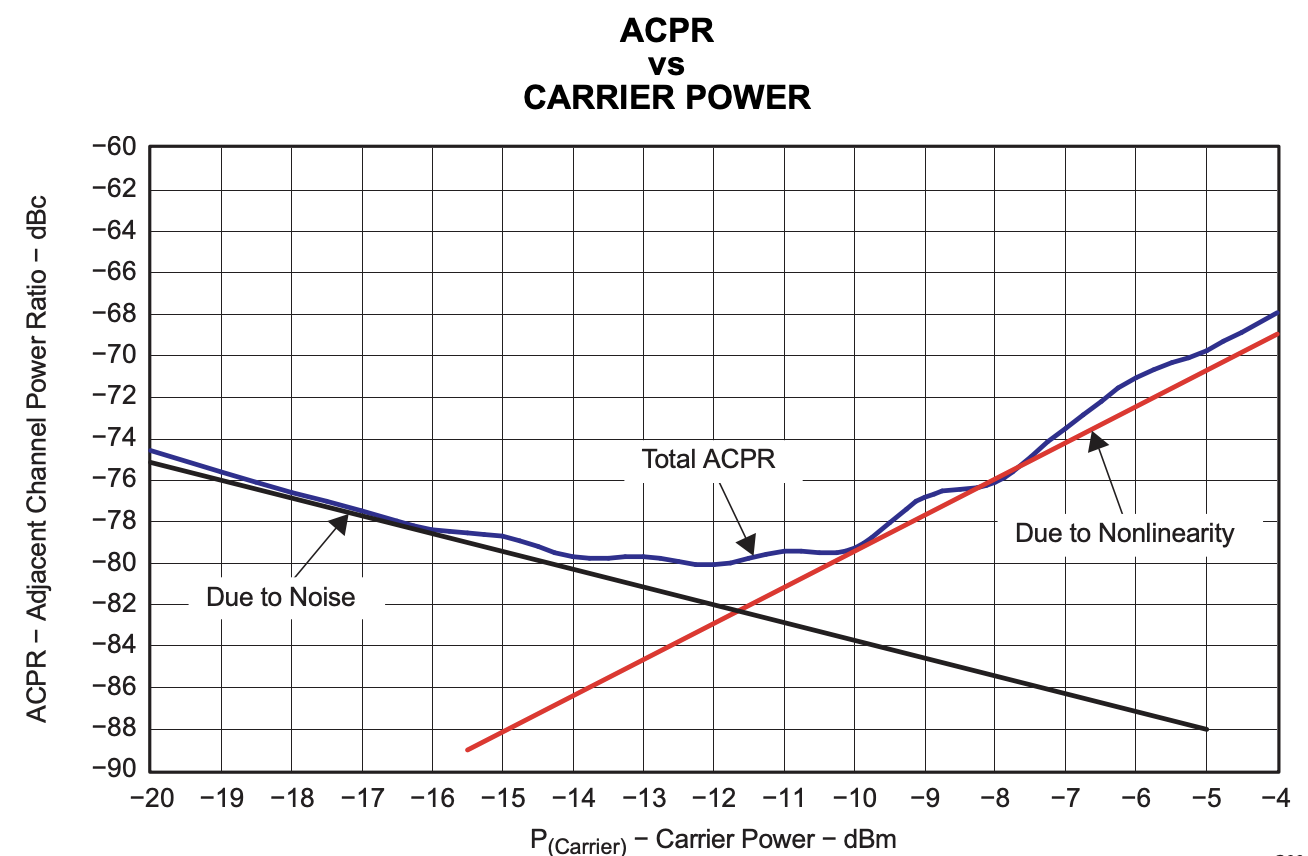
The ACPR varies with carrier power. At low carrier power, the ACPR is dominated by noise and at higher carrier power, ACPR is dominated by spectral regrowth due to nonlinearities.