What is astable multivibrator?
Astable Multivibrators are auto-triggered multivibrators. Since these are automatically triggered, they behave as an oscillator. An electronic circuit that generates square waves (or other non-sinusoidal such as rectangular, saw-tooth waves) is known as a multivibrator. The name astable is derived because both states are unstable.
How to design a astable multivibrator?
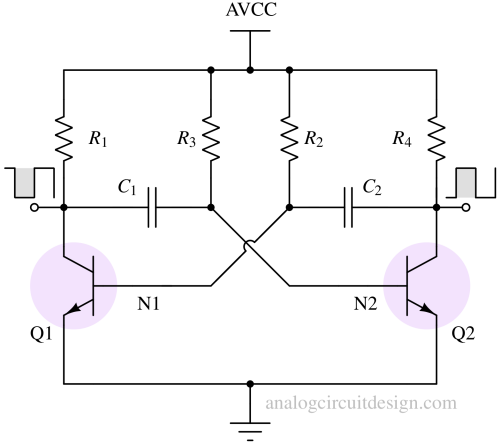
An astable multivibrator, as shown in the figure above, is basically two CE amplifier circuits arranged with positive feedback. At a time, one of the amplifiers is conducting (Saturated) while the other is cut off. After a certain amount of time (called the time period of oscillation), the circuit conditions reverse, with the saturated transistor turning off and the cut-off transistor turning on.
Usually, R1 = R4 = RL, R2 = R3=R, C1 = C2 = C, and Q1 is identical to Q2. Also, RL << R.
How the astable multivibrator works?
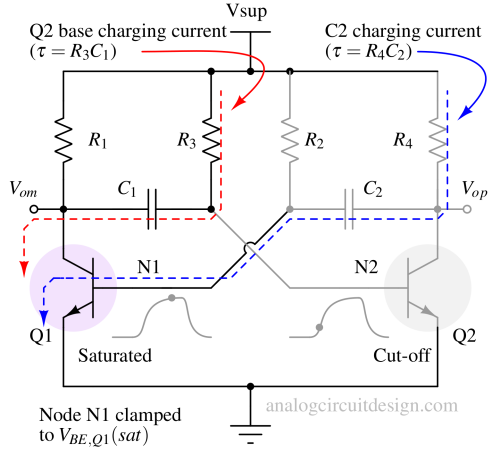
When the circuit starts up, due to some natural noise and mismatch, one of the transistors will be cut off and another one is in saturation.
Let’s assume an initial state where Q1 is turned on (saturation) and Q2 is turned off (cutoff). The right plate of the capacitor C1 is node N2 which is connected to the base of Q2 and is becoming positive. After a certain period of time, the base of Q2 will become sufficiently positive to cause Q2 to change states from cutoff to conduction. This will pull down the node Vout and immediately turn off Q1 (voltage across the capacitor does not change instantaneously). The left plate of capacitor C2 was at VBE,Q1(sat) and the right plate was at AVCC just before Q2 turned on. The time it took for Q2 to remain in the cutoff and then become saturated is determined by the time constant R3C1.
Derivation of frequency in astable multivibrator
We assume a condition where Q1 has just turned on. Just before Q1 turned on, the voltage across C1 is :
As soon as Q1 is turned on, Vom is VCE-Q1,sat (~ 0V). It will take some time (τ) to reach VBE,Q2 as per the following equation:
Since the node N2 could reach AVCC (it does not know that it will saturate to VBE,Q2)
Transistor Q2 will turn on as soon as VC1 reaches VBE,Q2. So, we can rewrite VC1 as :
Since,
$$V_{CE-Q1,sat}\simeq{}0$$
$$AVCC\gg{}V_{BE,Q2}$$
The above equation could be re-arranged to:
$$AVCC=2\cdot{}AVCC\cdot{}e^{-\tau{}/R_3C_1}$$
$$\implies{}\tau{}=\ln{(2)}\cdot{}R_3\cdot{}C_1$$
As soon as Q2 turns on, Q1 will turn off which marks one half-cycle. For the other half, the time is :
$$\tau{}=\ln{(2)}\cdot{}R_2\cdot{}C_2$$
So, the total time period is :
$$Freq = \cfrac{1}{2\ln{(2)}\cdot{}R\cdot{}C}=\cfrac{1}{1.38RC}$$
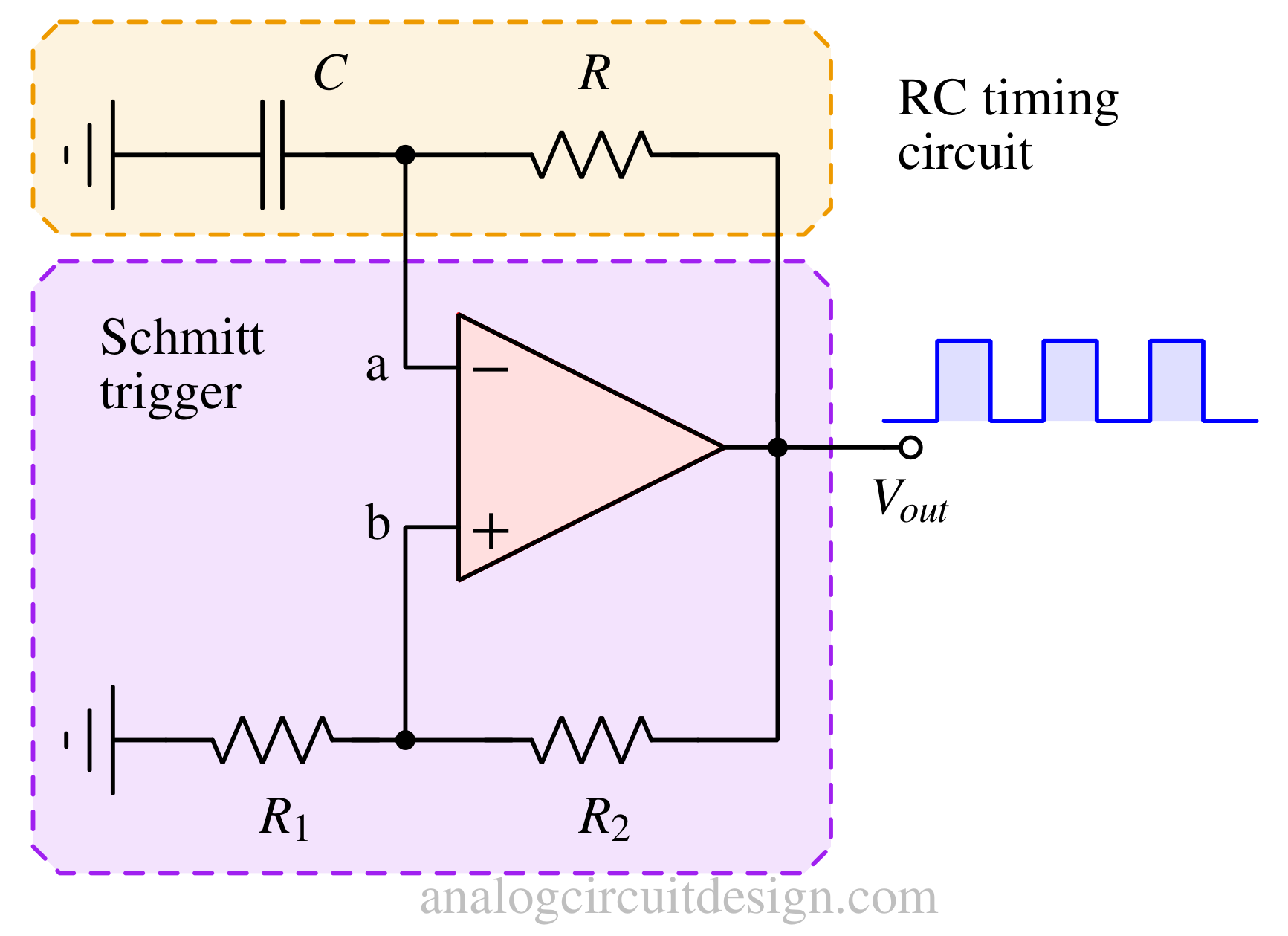
How to design opamp based astable multivibrator?
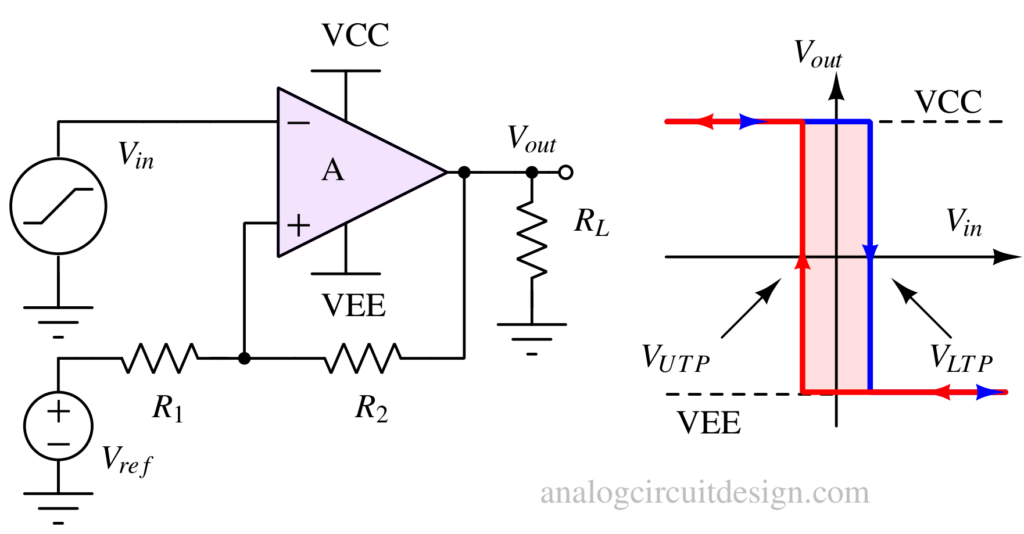
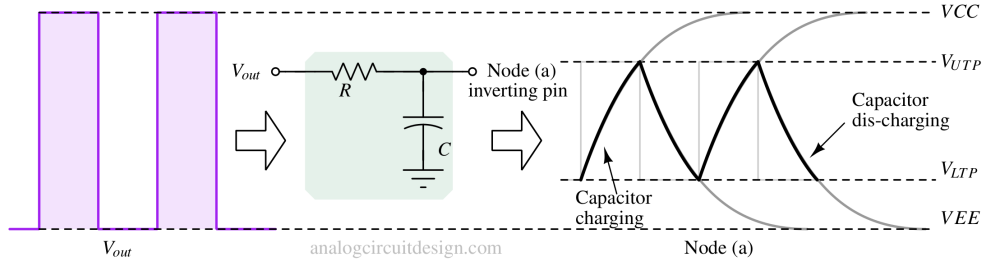
The op-amp comparator circuit in Fig 3 is configured as a Schmitt trigger that uses positive feedback provided by resistors R1 and R2 to generate hysteresis. These hysteresis voltages are utilized as timing thresholds to make an oscillator. An RC network is added (shown in Fig 4) which adds delay from the output pin to the inverting pin.
As soon as the upper threshold is met by the inverting pin, the output goes to VEE, and the inverting pin starts to follow. Now after some time, the inverting pin hits the lower threshold due to which output goes to VCC. This back-and-forth between VCC and VEE continues with the time period it takes for the inverting pin to hit the thresholds.
$$T_{period}=2RC\ln{\left(1+2\cfrac{R_2}{R_1}\right)}$$
The above expression can derived from Fig 5, considering the fact that VCC=-VEE and charging and discharging time constants are identical.
Designing astable multivibrator using Timer-555 IC
The 555 timer functions as an oscillator, generating a continuous square wave output. To learn more about the astable multivibrator mode in it, please visit this page – Timer 555
What are the applications of astable multivibrator?
- LED Flashers: Astable multivibrators are frequently used to create LED flasher circuits for decorative lighting, warning indicators in vehicles and roads, and other visual alerts. By adjusting the resistor and capacitor values, you can control the flash rate of the LEDs.
- Tone Generation: Astable multivibrators can be used to produce audio tones in applications such as alarms, sirens, musical instruments, and sound effects generators.
- Pulse Generators: They can serve as pulse generators in various applications where precise timing and repetition rates are needed, such as in digital logic circuits.
- Clock Source: Astable multivibrators can be used to generate clock signals in digital circuits, microcontrollers, and other timing-sensitive applications.
- Frequency Modulation (FM): In some communication systems, astable multivibrators can be used to generate FM signals. By modulating the input voltage, you can vary the frequency of the output waveform.
- PWM (Pulse-Width Modulation) Generation: Astable multivibrators are employed in PWM controllers to regulate the duty cycle of a square wave output. This is useful in motor speed control, LED dimming, and other applications requiring precise pulse-width control.
- Motor Speed Control: In conjunction with additional circuitry, astable multivibrators can be used to control the speed of DC motors by adjusting the duty cycle of the output signal.
