Basic Digital Logic Gates¶
Digital logic gates are fundamental building blocks in digital circuitry used to perform logical operations on binary inputs (zeros and ones) to produce binary outputs. These gates implement Boolean functions and implement more complex digital circuits. They can be interconnected in various ways to perform arithmetic, control, and memory functions, allowing the creation of processors, memory units, and other digital devices. Also, read about transistors which are used to create these logic gates.
There are several types of logic gates which are listed in the following article:
Discrete logic gates ICs¶
| Sr. No. | Logic | TTL/BJT | CMOS |
|---|---|---|---|
| 1 | AND | 7408 | 4081 |
| 2 | OR | 7432 | 4071 |
| 3 | NOT | 7404 | 4069 |
| 4 | NAND | 7400 | 4011 |
| 5 | NOR | 7402 | 4001 |
| 6 | XOR | 7486 | 4070 |
| 7 | XNOR | 74266 | 4077 |
Fundamental logic gates¶
Fundamental logic gates are as follows:
- NOT gate
- AND gate
- OR gate
- XOR gate
NOT gate¶
A NOT gate, also known as an inverter, is a fundamental digital logic gate that performs the logical negation of its input. In simpler terms, it takes an input signal and produces an output signal that is the opposite (complementary) of the input signal.
| A | Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
Working principle:
- If the input to the NOT gate is logic high (1), the output is low (0).
- If the input to the NOT gate is logic low (0), the output is high (1).
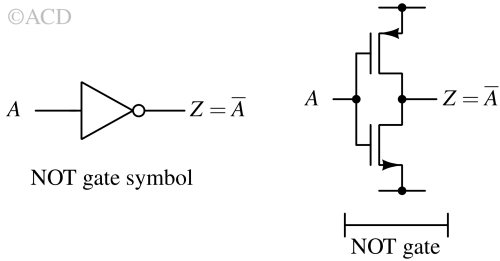
The symbol for a NOT gate typically looks like a triangle with a small circle at its input side, representing negation. This gate is essential in digital circuit design as it allows for logical operations such as inversion, which are crucial in constructing more complex circuits.
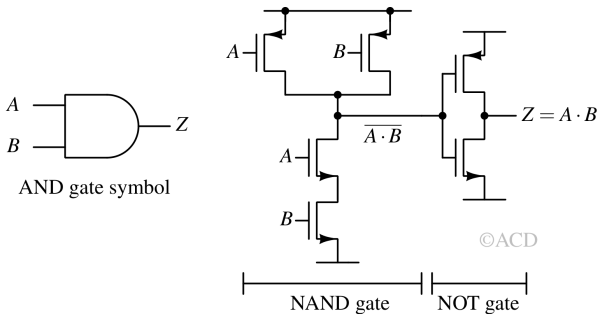
AND gate¶
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
An AND gate is another fundamental digital logic gate that produces an output signal only when all its inputs are high (1 or True).
Working principle:
- If both inputs to the AND gate are high (1), the output is high (1).
- If any input to the AND gate is low (0), the output is low (0).
The symbol for an AND gate usually consists of a shape with two inputs and one output. It often looks like a D or wedge shape. In digital circuit design, AND gates are essential for combining multiple signals so that the output is logic-high only when all inputs are logic-high. They're fundamental in constructing logical operations and data processing circuits.
NAND gate¶
A NAND gate is a digital logic gate that operates the logical NOT-AND. It produces an output that is the opposite of the AND operation. In other words, it only gives a high output (1) when at least one of its inputs is low (0).
| A | B | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Working principle:
- If both inputs to the NAND gate are high (1), the output is low (0).
- If any input to the NAND gate is low (0), the output is high (1).
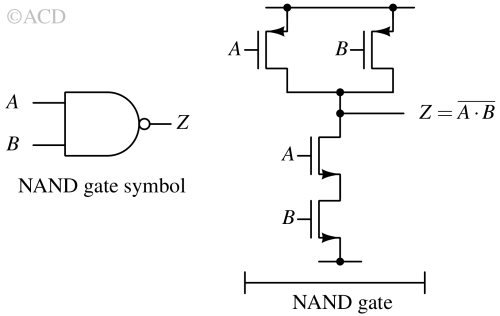
The symbol for a NAND gate is similar to an AND gate, but with a small circle (representing the NOT operation) at the output. It usually has two input terminals and one output terminal.
NAND gates are fundamental in digital circuit design and are often used to construct more complex logic functions due to their versatility. In fact, any other logical function can be implemented using just NAND gates, making them a cornerstone in digital logic design.
OR gate¶
An OR gate is a fundamental digital logic gate that performs the logical OR operation. It produces an output signal when at least one of its inputs is high (1).
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Working principle:
- If either or both inputs to the OR gate are high (1), the output is high (1).
- The output is low (0) only when both inputs are low (0).

The symbol for an OR gate usually consists of a shape with two inputs and one output, similar to an AND gate. However, the shape typically has a curved line instead of a straight line, representing the OR operation.
OR gates are essential in digital circuit design for combining multiple signals in a way that the output is true if at least one input is true. They are used in various applications, including in arithmetic logic, data processing, and control systems.
NOR gate¶
A NOR gate is a fundamental digital logic gate that performs the logical NOR (NOT-OR) operation. It produces an output signal only when both its inputs are low (0).
| A | B | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Working principle:
- If both inputs to the NOR gate are low (0), the output is high (1).
- If either or both inputs to the NOR gate are high (1), the output is low (0).
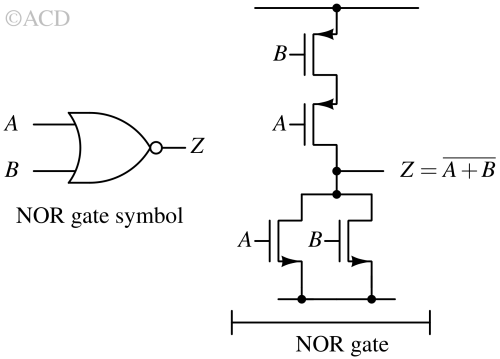
The symbol for a NOR gate typically looks like an OR gate with a small circle at its output, indicating the negation operation.
Due to their versatility, NOR gates are widely used in digital circuit design, often in combination with other gates. They can be used to construct various logic functions and are particularly useful in situations where multiple inputs need to be considered together.
XNOR gate¶
An XNOR gate, or an exclusive NOR gate, is a digital logic gate that produces a high output only when both inputs are the same (high or both low). For more than two input XNOR gates, if the inputs have an even number of highs, then the output is high.
| A | B | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Working principle:
- If both inputs to the XNOR gate are the same (high or both low), the output is logic high (1).
- If the inputs to the XNOR gate are different (high and low), the output is logic low (0).
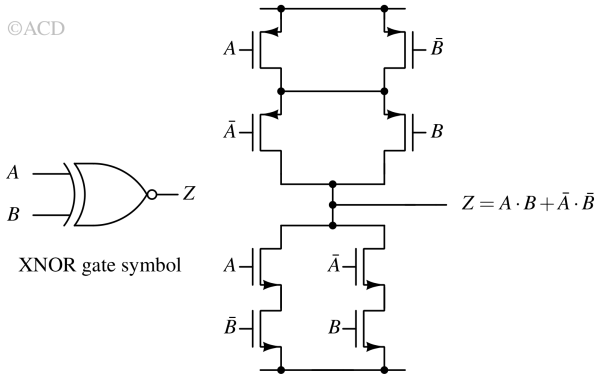
In essence, the XNOR gate performs the opposite operation of the XOR gate. The XNOR gate is essentially an XOR gate followed by a NOT gate. The symbol for an XNOR gate usually looks like an XOR gate with a small circle at its output, indicating the negation operation. XNOR gates are commonly used in digital circuit design applications, including comparing two binary values or implementing some flip-flops and latch circuits.
XOR gate¶
An XOR gate, short for Exclusive OR gate, is a fundamental digital logic gate that produces a high output (1) only when the number of high inputs is odd.
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Working principle:
- If the number of high inputs is odd, the output is high (1).
- If the number of high inputs is even, the output is low (0).
In other words:
- If both inputs to the XOR gate are different (one high and one low), the output is high (1).
- If both inputs to the XOR gate are the same (both high or both low), the output is low (0).

The symbol for an XOR gate typically consists of a shape with two inputs and one output, and it often looks like the letter "X" with a curved line at the intersection.
XOR gates are widely used in digital circuit design for various applications, including arithmetic operations, error detection, and data encryption. They are fundamental components in building digital systems and are essential in many electronic devices and systems.
How logic gates are made?¶
Differing voltage levels represent high or low binary states in digital circuits. Typically, in most logic gates, a low state registers around zero volts (0 V), while a high state measures around positive +5V or +3.3V.
Logic gates are constructed using resistors, transistors, or diodes. Resistors often serve as pull-up or pull-down resistors. They're employed when unused inputs of logic gates need a connection to a logic level of 1 or 0, preventing unintended gate switching. Pull-up resistors link to Vcc (+5V), while pull-down resistors connect to ground (0 V).
Two commonly utilized types of logic gates are TTL (Transistor-Transistor Logic) and CMOS (Complementary Metal-Oxide-Silicon). TTL ICs utilize NPN and PNP Bipolar Junction Transistors, commonly found in the 7400 series of chips. CMOS ICs, constructed from MOSFET or JFET Field Effect Transistors, are frequently labeled in the 4000 series of chips.