Butterworth, Chebyshev & Bessel filters¶
The Butterworth, Chebyshev, and Bessel filters are the three primary "classical" approximations, each optimized for a specific performance characteristic.
Butterworth filter response¶
A Butterworth filter has a frequency response that is as flat as possible in the passband but a relatively slow and monotonic transition from the passband to the stopband. It also has a moderate phase distortion. Butterworth filters have poles that lie on a circle in the complex plane.
Key characteristics of a Butterworth filter include:
- Flat Frequency Response: In the passband, a Butterworth filter aims to maintain a constant amplitude response, which means that it doesn't introduce ripples or variations in the amplitude of the passed frequencies.
- Slow Roll-Off: The transition between the passband and stopband is gradual and smooth, which means that the attenuation of frequencies outside the passband occurs at a slower rate compared to some other filter types like Chebyshev or Elliptic filters. This slow roll-off is a trade-off for the flatness of the passband response.
- Maximally Flat Response: A Butterworth filter is often referred to as a "maximally flat magnitude response" filter because it provides the maximum possible flatness in the passband without introducing ripples.
The order of a Butterworth filter determines how quickly the frequency response rolls off into the stopband. Higher-order Butterworth filters have steeper roll-off characteristics. The order is typically denoted by "n," and a higher "n" corresponds to a steeper roll-off. For example, a first-order Butterworth filter has a 20 dB/decade roll-off, a second-order has a 40 dB/decade roll-off, and so on.
It is named after Stephen Butterworth for explaining the behavior in this paper.
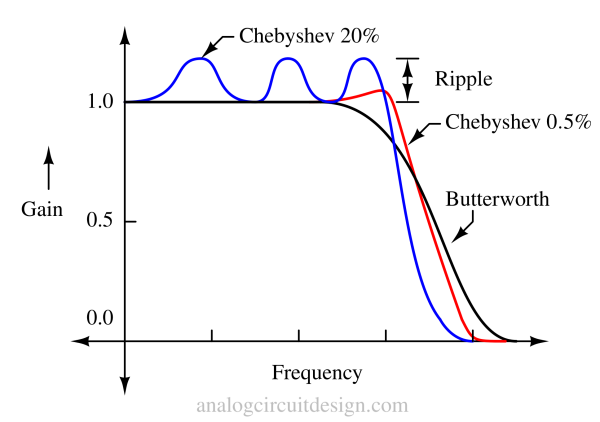
Fig 1, shows a comparison between Chebyshev and Butterworth low pass filters. The roll-off is sharper in Chebychev but with ripples in the pass band. The Butterworth has a smooth roll-off without ripples in the passband or stop band.
Chebychev filter response¶
Chebyshev filters achieve a faster roll-off by allowing ripple in the passband. This gain ripple, expressed in dB, is an adjustable parameter in filter design. Poles of a Chebyshev filter lie on an ellipse in the complex plane.
Key characteristics of Chebyshev filters include:
- Ripple in the Passband: Unlike Butterworth filters, which aim for a maximally flat passband response, Chebyshev filters deliberately introduce controlled ripple in the passband. This ripple allows Chebyshev filters to achieve a steeper roll-off while still maintaining a specified level of attenuation in the stopband.
- Adjustable Ripple: The amount of ripple in the passband is adjustable and can be controlled by a parameter known as the "ripple factor" or "Chebyshev ripple." This parameter allows the filter designer to trade off ripple for sharper roll-off characteristics.
- Steeper Roll-Off: Chebyshev filters provide a faster roll-off into the stopband compared to Butterworth filters of the same order. This means that they can quickly attenuate frequencies beyond the passband.
Chebyshev filters come in two main types:
- Chebyshev Type I: In Chebyshev Type I filters, the ripple occurs in the passband, making them suitable for applications where a specific frequency range needs to be emphasized while allowing some ripple.
- Chebyshev Type II: In Chebyshev Type II filters, the ripple occurs in the stopband, making them suitable for applications where it's critical to minimize signal distortion in the passband. These filters are often used in applications like anti-aliasing and reconstruction filters for analog-to-digital and digital-to-analog converters.
These filters are named after Chebyshev polynomials, developed by the Russian mathematician Pafnuti Chebyshev.
Bessel filter response¶
Bessel filters are designed to optimize maximally flat time delay, ensuring a constant group delay. This characteristic results in a linear phase response and an outstanding transient response to pulse inputs. However, this results in a flatter frequency response and a slow roll-off rate in the stop band.
Group delay quantifies a signal's time to traverse a network, indicating its transit time. Constant group delay within the passband, extending into the transition band, reflects a highly favorable step response. In the time domain (transient response), the input signal is replicated exactly with a delay. Generally, a filter's group delay is nearly directly proportional to its order and inversely proportional to its bandwidth. Bessel filters are exclusively available with low pass selectivity.
Comparison between Butterworth Chebyshev and Bessel filter¶
Butterworth filters demonstrate satisfactory amplitude and transient characteristics. Chebyshev filters enhance amplitude response but sacrifice transient behavior. In contrast, the Bessel filter prioritizes superior transient response by maintaining a linear phase vs frequency, resulting in constant delay across the passband. Consequently, this may lead to a comparatively reduced frequency response with less amplitude discrimination.
Schematic examples¶
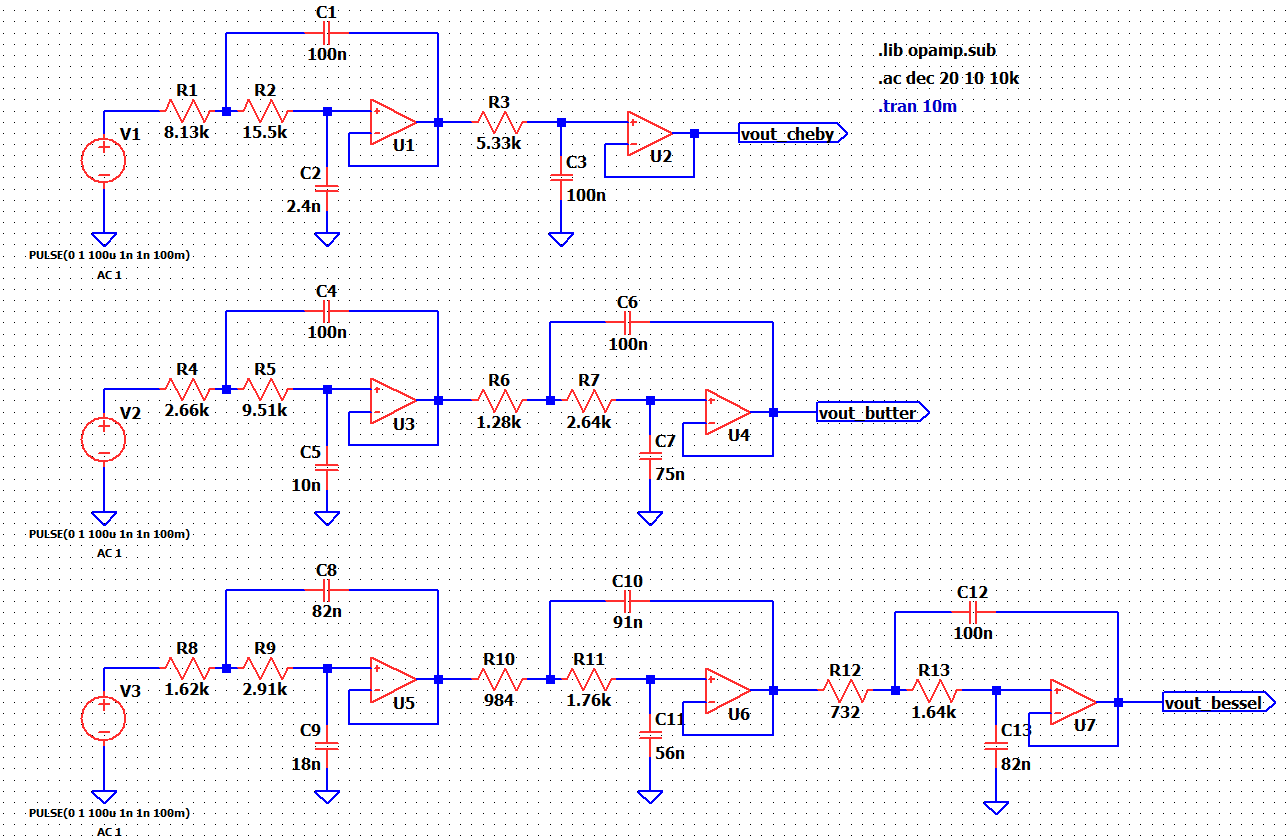
Passband : Gain = 0dB and -3dB cutoff frequency = 1kHz
Stopband : -40dB cutoff frequency = 4kHz
The top schematic shows the chebychev filter which has minimum number of components. In the middle, Butterworth filter is shown. It has moderate number of components. At the bottom, we have Bessel filter which has highest number of components.
This doesn't mean that Bessel filter is not good. In the following section we will see that the Bessel filter has the best transient response.
Transient (step response)¶
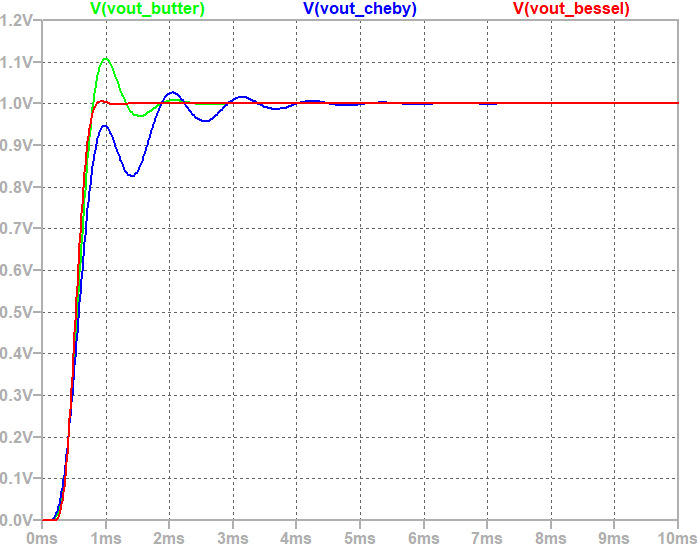
It can be observed that the Chebyshev filter takes longest to settle (~7ms) due to ringing nature in its step response. Butterworth filter takes a moderate time to settle (~3ms) with a single 10% overshoot. The Bessel filter takes minimum time to settle (~1ms) without any (or a negligible) overshoot.
Frequency response¶
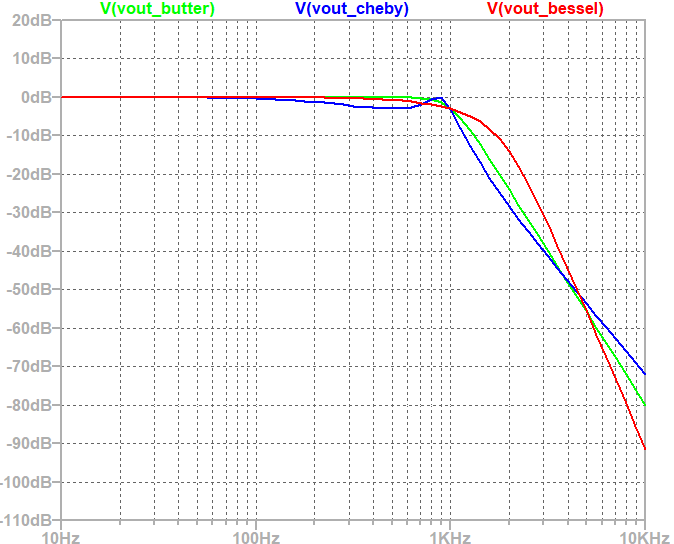
It can be observed that the Chebyshev filter (in blue) has the sharpest attenuation in the band of 1kHz to 4kHz. However, it comes with passband ripple. Butterworth (in green) is having a moderate attenuation however still very useful. It does not have any passband ripple. Bessel filter is having the least attenuation is the transition region (1kHz-4kHz).
Summary¶
| Butterworth | Bessel | Chebychev | |
|---|---|---|---|
| Passband ripple | No ripple | Moderate | Highest |
| Transient settling | Moderate | Fastest | Slowest |
| Transient response | Good | Best | Worst |
| Transition band attenuation | Good | Worst | Best |
| Components requirement | Moderate | Highest | Lowest |
To achieve the desired responses we need to choose the type of active filter (Sallen-key, Multifeedback, Biquad etc). Any of these topologies can be used to realize Butterworth, Chebychev or Bessel filters.
Butterworth and Chebyshev filters are special cases of elliptical filters. With zero ripples in the stopband but ripple in the passband, an elliptical filter becomes a Type I Chebyshev filter. With zero ripples in the passband but ripples in the stopband, an elliptical filter becomes a Type II Chebyshev filter. With no ripple in either band, the elliptical filter becomes a Butterworth filter. With ripple in both the passband and stopband, the transition between the passband and stopband can be steeper.
All-pole configurations, characterized by the absence of zeros in the transfer function, ensure the absence of ripple in the stop band. Butterworth and Bessel filters are prime examples of such configurations, exhibiting no ripple in the pass band.