Series combination of Capacitors
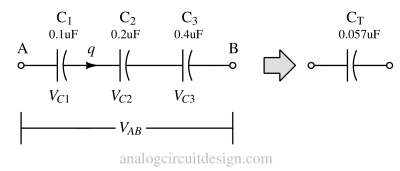
A series combination of capacitors involves connecting multiple capacitors end-to-end to share the same path for electric charge, resulting in a single pathway. In a series configuration, the charge stored in each capacitor is the same, so the total voltage is the sum of the voltage across each capacitor. A capacitor with higher capacitance will have a lower voltage drop across it, and vice versa.
Total Capacitance: The formula to calculate the total capacitance (Ctotal) in series is the reciprocal of the sum of the reciprocals of individual capacitances (C1, C2, C3, …):
$$\cfrac{1}{C_{total}}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}+\cdots{}$$
Derivation:
Using KVL,
$$V_{AB}=V_{C1}+V_{C2}+V_{C3}$$
Because the same amount of charge q is flowing from each capacitor, replacing q=CV relationship in the above equation,
$$\cfrac{q}{C_{total}}=\cfrac{q}{C_1}+\cfrac{q}{C_2}+\cfrac{q}{C_3}$$
$$\implies{}\cfrac{1}{C_{total}}=\cfrac{1}{C_1}+\cfrac{1}{C_2}+\cfrac{1}{C_3}$$
Equivalent Capacitance: The equivalent capacitance in a series combination is always smaller than the smallest individual capacitance. Adding more capacitors in series increases the distance between the plates, reducing the overall ability to store charge.
Parallel combination of Capacitors
A parallel combination of capacitors involves connecting the plates of multiple capacitors together at the same voltage level, essentially creating multiple pathways for electric current. In this configuration, all the positive plates are connected together, and all the negative plates are connected together. In a parallel configuration, all capacitors have the same voltage across them. Capacitors with larger capacitance can store more charge than those with smaller capacitance values.
Total Capacitance: The total capacitance (CT) of capacitors in parallel is the sum of the individual capacitances (C1, C2, C3, …):
$$C_{T}=C_1+C_2+C_3+\cdots{}$$
Derivation:
The total charge from CT should be equal to the sum of individual charges in each capacitor because we are trying to replace all the capacitors with a single capacitor,
$$Q=q_{1}+q_{2}+q_{3}$$
Because every capacitor has the same voltage VAB, we can use the relation q=CV and replace the terms in the above equation,
$$C_TV_{AB}=C_1V_{AB}+C_2V_{AB}+C_3V_{AB}$$
$$\implies{}C_T=C_1+C_2+C_3$$
Equivalent Capacitance: The equivalent capacitance in a parallel combination is always greater than the largest individual capacitance. This is because connecting more capacitors in parallel effectively increases the area of the plates, which enhances the overall ability to store charge.
Voltage Rating: When capacitors are connected in parallel, the voltage rating of the parallel combination is equal to or lesser than the lowest voltage rating among the individual capacitors. This prevents voltage breakdown issues.
Parallel combinations of capacitors are commonly used to increase the overall capacitance in electronic circuits, thereby enabling more charge storage and energy delivery capabilities.