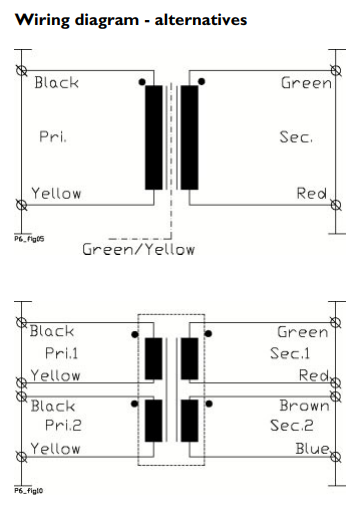
Transformer's dot notation¶
In transformer schematics, "dot" symbols are often placed on one end of the transformer windings. These symbols are placed according to the dot convention rule. The dot notation is used to identify the phase relation between primary and secondary current and voltage in a transformer.
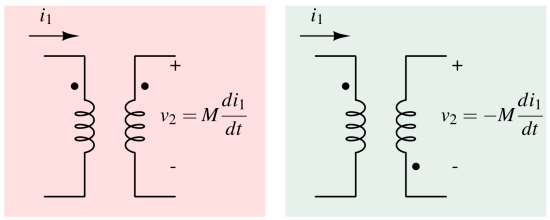
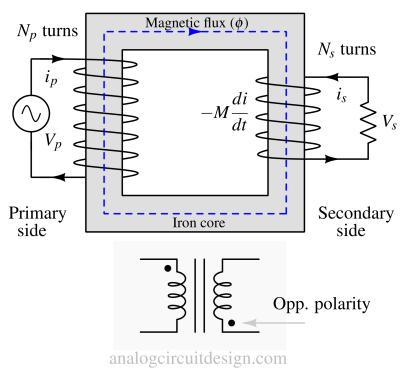
As shown in the above figure, if the current enters the dotted terminal of primary windings (coil/inductor), it induces a voltage at the secondary windings, which has positive polarity at the dotted terminal.
Why dot notation is important ?¶
Sometimes, dot notations are not used while using the circuit diagram of a transformer. That means both primary and secondary sides are in-phase.
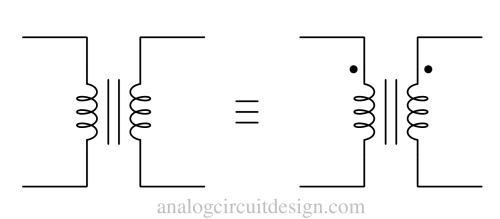
However, there can be cases where there are multiple secondary windings with different physical polarities. In such cases, dot-notation is very useful for identifying the polarity of each secondary side with respect to the primary side.

How is dot notation derived from a transformer?¶
Dot notation is derived from a transformer by examining the orientation in which both coils (primary and secondary) are physically wound. We must apply Lenz's law with the \right-hand rule to get the dot notation. Usually, manufacturers provide the dot notation with the transformers.
We should note that the primary winding and direction of the current on the primary side (ip) decide the direction of magnetic flux through the core.
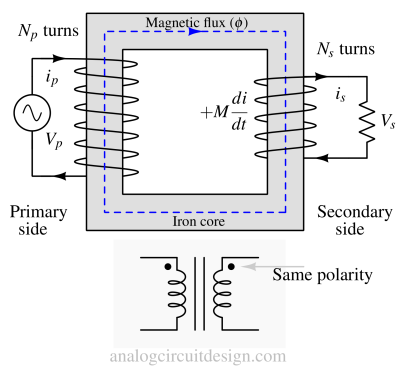
When the dots are placed next to the top ends of the primary and secondary windings as shown in Fig 4, it indicates that the polarity of the instantaneous voltage across the primary winding will be the same as that across the secondary winding.
This means that the phase shift between the primary and secondary winding will be zero (in phase), and the direction of the Secondary current (is) and Primary current (ip) will be the same.
If the dots are placed in crossed positions (e.g. up on primary, down on secondary, or vice versa), like mentioned in Fig 5, it indicates that the primary and secondary current and voltages are 180° out of phase and the primary and secondary currents (ip and is) will be in opposite in direction to one another.
The magnetic flux direction in Fig 5 is the same as in Fig 4 but the winding pattern is opposite, which means that the voltage induced across the load resistor would be opposite. So, we can assign the dot to the side of the load where positive voltage is getting induced.
Intuitive way to understand dot notation¶
Consider each transformer winding as a voltage source with no load. The dot notation shows the polarity of the voltage sources.
With loads (capacitive/resistive/inductive), the phase may not be exactly 0 or 180. So to make understanding simple, it is assumed that there is no load while finding the voltage polarity.
Application of dot notation¶
Dot notation eliminates confusion about the polarity of the secondary side of the transformer. If not used properly, an intentional series connection can become parallel or vice-versa.
The worst can happen if the secondary side of 2 different voltage levels is accidentally connected in parallel. Then, it can draw a large current, which can destroy the transformer.
Manufacturers provide proper dot notation in the transformer to eliminate any confusion.