Fermi energy level in semiconductors¶

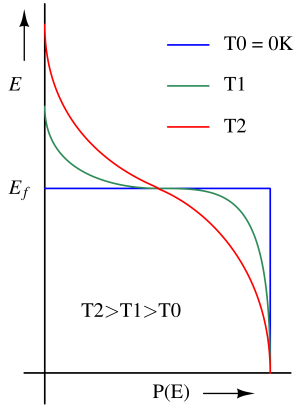
Fermi energy level (E_f) is the highest energy state where an electron can be present at 0K.  For higher temperatures, the probability, P(E) of finding an electron at energy level (E) above E_f starts to increase gradually as mentioned in Fig. 1. 

Following are some relations describing Fermi-energy level :

$$P(E) = \cfrac{1}{1+\exp{\left(\cfrac{E-E_f}{kT}\right)}}$$

Also known as Fermi-dirac distibution. An approximate equation can be derived from it if (E - E_f> 3kT).

$$P(E) \simeq{} \exp{\left(-\cfrac{E-E_f}{kT}\right)}$$

The above equation is also known as Boltzman distribution.

The probability function alone is not sufficient to tell the number of electrons. It is required to take into account the available number of states at energy level (E). There can't be an electron present if there is no state available even if the probability is very high. The probability will play a significant role only if states are already available. States are nothing but hybridized orbitals.

E_f can be manipulated using doping concentration and external voltage bias. Please note that E_f is only an indicative energy level (not a physically existing energy level). It may exist in the forbidden energy band also. For example, an intrinsic semiconductor's Fermi level E_fi lies slightly above the mid of E_c and E_v. 

$$E_{fi} = \cfrac{E_c+E_v}{2}+\cfrac{kT}{2}ln{\cfrac{N_v}{N_c}}$$

The above equation will be derived in next section.

Total carrier density due to Fermi-dirac distribution and available states¶

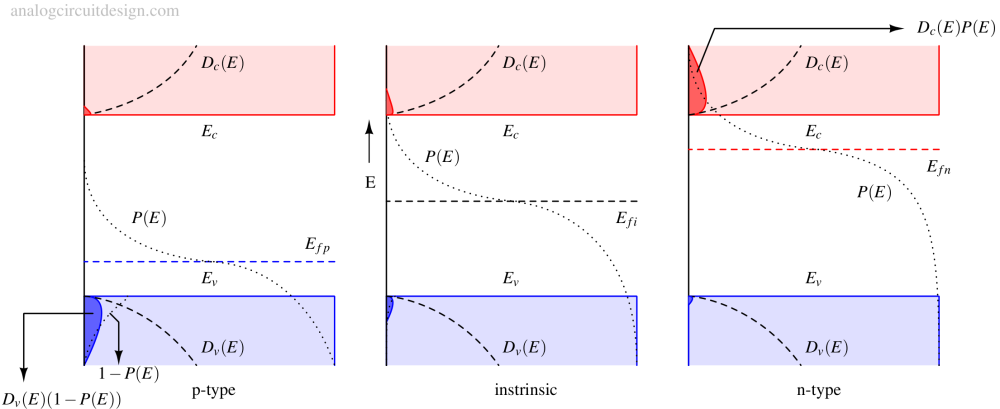
For the following derivations, please refer Fig. 2 for visualisation.

The density of states at a given energy level is given by following relations :

For conduction band,

$$D_c(E) = \cfrac{8\pi{}m_n\sqrt{2m_n\left(E-E_c\right)}}{h^3} ,E>E_c$$

For valence band,

$$D_v(E) = \cfrac{8\pi{}m_p\sqrt{2m_p\left(E_v-E\right)}}{h^3} ,E<E_v$$

So number of electrons ((n)),

$$n = \int_{E_c}^{\infty}D_c(E)P(E)dE = N_c.\exp{\left(\cfrac{E_f - E_c}{kT}\right)}$$

and number of holes ((p)),

$$p = \int_{0}^{E_v}D_v(E)(1-P(E))dE = N_v.\exp{\left(\cfrac{E_v - E_f}{kT}\right)}$$

N_c and N_v are maximum available states in conduction and valence band respectively.

From above equations,

$$p.n = N_cN_v\exp{\left(\cfrac{E_v-E_c}{kT}\right)} = N_cN_v\exp{\left(-\cfrac{E_g}{kT}\right)} = n_i^2$$

So, intrinsic carrier concerntration (n_i) comes out to be,

$$\implies{} n_i = \sqrt{N_cN_v}\exp{\left(-\cfrac{E_g}{2kT}\right)}$$

Where,

$$E_g = E_c - E_v$$

Instrinsic Fermi energy level¶

Intrinsic semiconductors (without doping) have an equal number of holes and electrons because the only source of electrons and holes is thermal generation. The opposite of thermal generation is called recombination. Thermal generation results in an equal number of electrons and holes in the semiconductor.

So,

$$n=n_i=p$$

From above carrier concentration relations,

$$N_c\exp{\left(\cfrac{E_{fi}-E_c}{kT}\right)} = n_i = N_v\exp{\left(\cfrac{E_v-E_{fi}}{kT}\right)}$$

$$E_{fi} = \cfrac{E_c+E_v}{2}+\cfrac{kT}{2}ln{\cfrac{N_v}{N_c}}$$

Effects of doping in Fermi energy level (Quasi fermi level)¶

The Fermi energy level of a doped semiconductor is called quasi-Fermi level.

With n-type doping, the extra electrons increase the probability of higher energy states being occupied. So, the fermi-level is raised towards the conduction band. More is the doping with donor atoms, closer the Fermi level moves toward the conduction band. We denote this quasi-fermi level by E_fn. 

For n-type semiconductor,

$$n = N_D = N_c.\exp{\left(\cfrac{E_{fn} – E_c}{kT}\right)} = N_c.\exp{\left(\cfrac{E_{fn} - E_{fi} + E_{fi} – E_c}{kT}\right)}$$

$$N_D=\underbrace{N_c.\exp{\left(-\cfrac{E_c – E_{fi}}{kT}\right)}}_{n_i}\exp{\left(\cfrac{E_{fn} – E_{fi}}{kT}\right)}$$

$$N_D=n_i\exp{\left(\cfrac{E_{fn} – E_{fi}}{kT}\right)}$$

$$\implies{} E_{fn} - E_{fi} = kTln{\left(\cfrac{N_D}{n_i}\right)}$$

With p-type doping, spaces previously occupied by silicon are now occupied by boron. So, there is a lesser electron density than the intrinsic density. Because of this scarcity of electrons in the p-type region, the probability to occupy even the intrinsic Fermi level E_fi decreases. So, the Fermi level moves down towards valence band E_v. We denote this quasi-fermi level by E_fp. For p-type semiconductor,

$$p = N_A = N_v.\exp{\left(\cfrac{E_{v} – E_{fp}}{kT}\right)} = N_v.\exp{\left(\cfrac{E_{v} - E_{fi} + E_{fi} – E_{fp}}{kT}\right)}$$

$$N_A=\underbrace{N_v.\exp{\left(-\cfrac{E_{fi} – E_{v}}{kT}\right)}}_{n_i}\exp{\left(\cfrac{E_{fi} – E_{fp}}{kT}\right)}$$

$$N_A=n_i\exp{\left(\cfrac{E_{fi} – E_{fp}}{kT}\right)}$$ $$\implies{} E_{fi} - E_{fp} = kTln{\left(\cfrac{N_A}{n_i}\right)}$$

In the case of intrinsic semiconductors, to achieve some conduction without doping, it will require a high temperature to spill more electrons above (E_c).

Effects of external voltage bias in Fermi energy level¶

Electrons are attracted towards positive potential. So, electrons will get into a lower energy state (more stable) when a positive potential is applied. So, the probability of finding electrons at a higher energy state reduces. Therefore the Fermi energy level E_f also drops. If a negative potential is applied, then E_f rises. E.g., A voltage (V) is applied across an n-type semiconductor. In equilibrium and no-bias conditions, Fermi-level (E_{fn}) is constant throughout the material. E_fn will be lowest (E_fn - V) where the positive terminal of the battery is connected. It will gradually increase to E_f where the positive terminal of the battery is connected. This will cause a drift current to flow.