Electronic Oscillators

Condition for sustained Oscillations¶

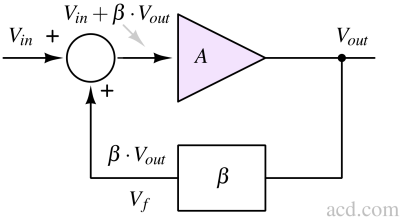
The overall transfer function from Vin to Vout is :

$$\cfrac{V_{out}}{V_{in}}=\cfrac{1}{1-A\cdot{}\beta{}}$$

As discussed in the article: Barkhausen criteria for harmonic oscillators, the one necessary condition to let the oscillation happen is getting infinite gain from input to output. This will lead to oscillations without any input signal (V_in=0):

$$\cfrac{V_{out}}{V_{in}}=\cfrac{1}{1-A\cdot{}\beta{}}\rightarrow{}\infty$$

$$\implies{}1-A\cdot{}\beta{}=0$$

$$\implies{}A\cdot{}\beta{}=1$$

If A.β < 1, the oscillations will eventually die down. If A.β > 1, the oscillation's amplitude will rise till it saturates the active element used in the circuit.

Types of oscillators¶

Harmonic oscillator¶

These are sinusoidal oscillators. Usually, these oscillators have active components in their linear region of operation. These oscillators' dynamic behavior is governed by a characteristic equation similar to simple harmonic motion (SHM) in objects.

$$L\cfrac{d^2i}{dt^2}+\cfrac{i}{C}=0$$

Examples of harmonics oscillators:

1. Wein Bridge Oscillator
2. RC phase shift Oscillator
3. Cross-coupled LC Oscillator
4. Colpitts Oscillator
5. Hartley Oscillator
6. Twin-T notch filter based oscillator

Relaxation oscillator¶

These are non-sinusoidal oscillators. Usually, these oscillators have active components which operate like switches. These oscillators produce the rectangular-wave, triangular-wave, etc., types of waveform.

Examples of Relaxation oscillators :

1. Astable multivibrator
2. RC relaxation oscillator
3. Timer 555 (astable multivibrator mode)