Kirchoff's circuit laws (KCL and KVL)¶
Kirchoff's law, along with Ohm's law, forms a powerful toolset to analyze circuits. Most of the circuits can be analyzed using these laws alone. Kirchoff's laws were introduced by the German physicist Gustav Robert Kirchoff. These laws are formally known as Kirchoff's current law (KCL) and Kirchoff's voltage law (KVL).
Kirchoff's current law (KCL)¶
Kirchoff's current law (KCL) states that the algebraic sum of currents entering a node is zero. It is based on the conservation of charge, which requires that the total charge of a node cannot change.
Mathematically it is represented as,
$$i_1+i_2+i_3+\cdots{}+i_n=0$$
Current entering a node may be regarded as positive and while current leaving the node can be regarded as negative.

Kirchoff's voltage law (KVL)¶
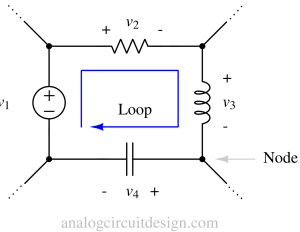
Kirchhoff's Voltage Law states that the sum of the voltages around any closed circuit loop equals zero.
This law is based on the energy conservation principle in electrical circuits. It implies that the total energy supplied by the voltage sources in a closed loop equals the total energy consumed by the circuit elements (resistors, capacitors, inductors, etc.) in that loop.
$$V_1+V_2+V_3+\cdots{}+V_n=0$$
Common circuit theory keywords¶
Branch¶
A branch represents a single element such as voltage/current source, resistors/capacitors/inductors etc.
Node¶
A node is a point in a circuit where two or more branches connect. An easy way to identify a node is to locate a wire where multiple electronics components are connected.
Loop¶
A loop is any closed path in a circuit. A single electronic component won't be considered twice.
Relation between Branch, Node and Loop¶
A network with B branches, N nodes, and L independent loops will satisfy the fundamental theorem of network topology:
$$B=L+N-1$$