Maximum power transfer theorem¶
The maximum power transfer theorem states, "The maximum amount of power will be dissipated by a load when it is equal to the Thevenin/Norton resistance of the network supplying the power."
A voltage source in real circuits has a series resistance, limiting the maximum current. Because of this series source resistance, the power through a load cannot be infinite. Usually, this theorem is applicable when the source resistance is known and cannot be changed. Therefore, we need to match the load with the source resistance to achieve maximum power out of a fixed source resistance voltage source. However, to achieve maximum efficiency, there is no other way than to reduce the source resistance.
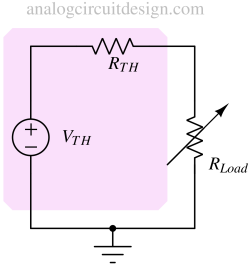
In the above figure, the source resistance is represented by RTH. The circuit highlighted is the Thevenin equivalent circuit of a complex circuit.
Proof of maximum transfer theorem¶
Power is delivered to the load,
$$P=\cfrac{V_{TH}^2R_{Load}}{\left(R_{TH}+R_{Load}\right)^2}$$
To find the maximum power, we need to differentiate the power with respect to variable load,
$$\cfrac{dP}{dR_{Load}}=\cfrac{V_{TH}^2}{\left(R_{TH}+R_{Load}\right)^3}\left(R_{TH}-R_{Load}\right)=0$$
$$\implies{}R_{Load}=R_{TH}$$
So, to achieve peak power from a circuit with source resistance as RTH, we need to have a load (RLoad) equal to RTH.
Power vs. load curve¶
When the load is zero, the power is zero. It increases with an increase in load till it reaches its peak. After the peak, the current start dropping because the load is increasing. The power through the load versus load resistance is mentioned in Fig 2.
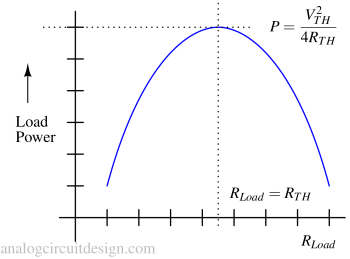
The power dissipated through the load when source resistance is zero¶
When the source resistance is zero, the entire voltage appears across the load because RTH is zero. So, as per the relationship,
$$P=\cfrac{V_{TH}^2}{R_{Load}}$$
So, the power through the load increase with a decrease in load resistance.