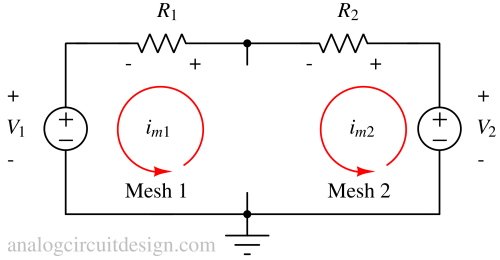
Mesh analysis¶
Mesh analysis system determines the current and voltage of elements inside a circuit using KVL. As shown in the example, there are fewer mesh currents than the number of branch currents, so mesh analysis is more straightforward than using KCL and KVL directly. Finding branch currents is relatively easier after the mesh currents are determined.
Step 1: Identify and label the meshes¶
What is a mesh?
A 'mesh' is a path through a circuit that starts and ends at the same place without taking an electronic component more than once. It is also called a loop.
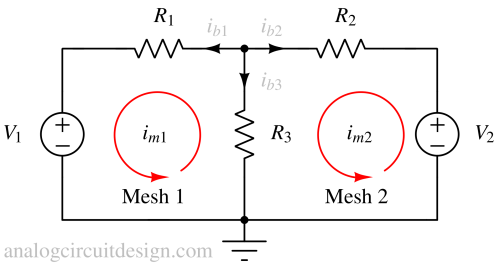
Step 2: Label the voltage drop polarities¶
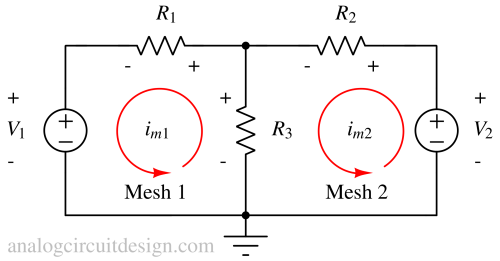
Step 3: Apply KVL in each mesh¶
$$V_1-i_{m1}R_1-(i_{m2}-i_{m1})R_2=0$$
$$V_2-i_{m2}R_2-(i_{m2}-i_{m1})R_3=0$$
Step 4: Solve the simultaneous mesh equations¶
$$i_{m1}=\cfrac{V_2R_3-V_1(R_2+R_3)}{R_1R_2+R_1R_3+R_2R_3}$$
$$i_{m2}=\cfrac{V_1R_3-V_2(R_1+R_3)}{R_1R_2+R_1R_3+R_2R_3}$$
Step 5: Retrieve branch currents and calculate voltage drops¶
If, V1\=20V, V2\=10V, R1\=40Ω, R2\=20Ω, R1\=10Ω then,
$$i_{m1}=-\cfrac{5}{14},\text{A}$$
$$i_{m2}=-\cfrac{3}{14},\text{A}$$
$$i_{b1}=i_{m1}=-\cfrac{5}{14},\text{A}$$
$$i_{b2}=-i_{m2}=\cfrac{3}{14},\text{A}$$
$$i_{b3}=i_{m2}-i_{m1}=\cfrac{2}{14},\text{A}$$
Special case¶
Supermesh¶
The condition for super mesh occurs when a current source is shared between 2 meshes. The current source is removed to analyze the mesh, and a single (super) mesh is formed.
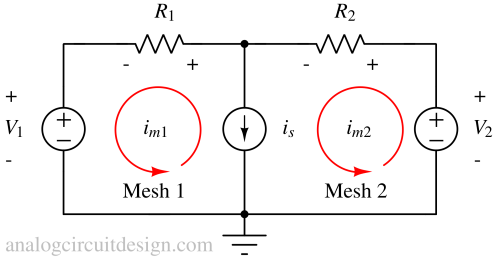
While analyzing, it can be assumed that the current source is not there. The detail of the current source being there is captured below,
$$i_s=i_{m2}-i_{m1}$$
The second equation would be the super-mesh loop,
$$V_2-i_{m2}R_2-i_{m1}R_1-V_1=0$$