What is Phase margin and Gain margin?
Phase margin and gain margin are the key metrics to quantify the stability of a system in frequency domain analysis. These metrics gauge a system’s proximity to instability and its potential for gain or phase adjustment before destabilization, offering engineers valuable insights for maintaining system stability while fulfilling performance and robustness criteria.
How to quantify stability of a system?
In this section, we will see how we quantify the stability of a linear negative feedback system. We will reuse the model mentioned in the article – Fundamentals of negative feedback systems. The transfer function is :
$$\cfrac{y(s)}{x(s)}=\cfrac{K(s)G(s)}{1+K(s)G(s)H(s)}$$
and the error transfer function is :
$$\cfrac{e(s)}{x(s)}=\cfrac{1}{1+K(s)G(s)H(s)}$$
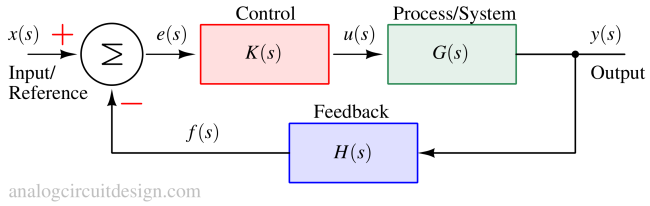
Let’s define the loop-gain transfer function to be LG(s) which is K(s)G(s)H(s). The error transfer function can be re-written in terms of LG(s) as:
$$\cfrac{e(s)}{x(s)}=\cfrac{1}{1+LG(s)}$$
The system is unstable at a particular frequency, meaning the output can sustain itself without input. The output is uncontrolled and not bounded. This happens when the denominator is zero for a particular frequency in the transfer function.
$$1+K(s)G(s)H(s)=0 \hspace{0.5cm} \text{or} \hspace{0.5cm} 1+LG(s)=0$$
If we want the system to be stable across frequencies in a negative feedback system, we must ensure that 1+LG(s) is never zero at any frequency. If 1+LG(s) is zero, according to Barkhausen’s criteria, the system can oscillate. Oscillation is a highly undesirable condition in a negative feedback system. We have to avoid the following conditions,
$$LG(s)=-1$$
Or,
$$|LG(s)|=1 \hspace{0.5cm} \text{and} \hspace{0.5cm} \angle{}LG(s)=-180^o$$
|LG|=1 is called the magnitude condition. ∠LG=-180° is called the phase condition. Both conditions have to be checked simultaneously. To make sure that the loop-gain transfer function is not near -1, we need to quantify how far the loop gain is from -1. That quantification is done using Phase and Gain margin.
What is phase margin?
Phase margin measures how stable a control system is. It shows how far off the phase of the loop-gain transfer function, LG(s) is from -180 degrees at the Gain crossover frequency (GCF). It’s usually measured in degrees. Phase margin is typically expressed in degrees and is calculated by finding the phase difference between the loop-gain transfer function and -180 degrees at the GCF.
A positive phase margin means the system is stable, while a negative phase margin means it’s unstable. The larger the positive phase margin, the more stable the system is.
Formula to calculate phase margin (PM):
$$\text{PM}=\angle{LG(j\omega{}_{GCF})}-(-180^o)=\angle{LG(j\omega{}_{GCF})}+180^o$$
What is Gain crossover frequency (GCF)?
It refers to the frequency at which the magnitude (gain) of the open-loop transfer function of a control system becomes equal to 1 or 0 dB. In other words, it is the frequency at which the system’s response is neither amplified nor attenuated, and it has a gain of 1. It is also called Unity gain frequency (UGF) or Unity gain bandwidth (UGB).
What is gain margin?
The gain margin is another stability measure used in control systems. It represents how much the gain of the loop-gain transfer function, LG(s) can be increased without causing the system to become unstable. A positive gain margin indicates stability, while a negative gain margin suggests that the system is unstable. Larger gain margins imply greater stability.
The gain margin is typically expressed in decibels (dB) and is calculated by finding the gain (magnitude) of the loop-gain transfer function at the Phase crossover frequency (PCF). The gain margin is the amount by which this gain can be increased before instability occurs.
Formula to calculate Gain margin:
$$\text{GM}=\cfrac{1}{|LG(j\omega{}_{PCF})|}$$
or if it is expressed in dB, then:
$$\text{GM (dB)}=0\,\text{dB}-20\log_{10}\left(|LG(j\omega{}_{PCF})|\right)$$
What is Phase crossover frequency (PCF)?
It represents the frequency at which the phase of the open-loop transfer function of a control system reaches -180 degrees.
Example to calculate gain and phase margin
To calculate the gain and phase margin, we shall first calculate the Gain crossover frequency and Phase crossover frequency of the transfer function. Let’s take a function LG(s):
$$LG(s)=100\cfrac{1+s/10}{(1+s/3)(1+s/100)}$$
The bode plot is an easy graphical method to find the Gain cross-over frequency as shown in Fig 5. The estimated frequency at which the gain is crossing 0dB is 3.5k rad/sec. At this frequency, the phase is -90°. So, the Phase margin is :
$$\text{PM}=180^o-90^o=90^o$$
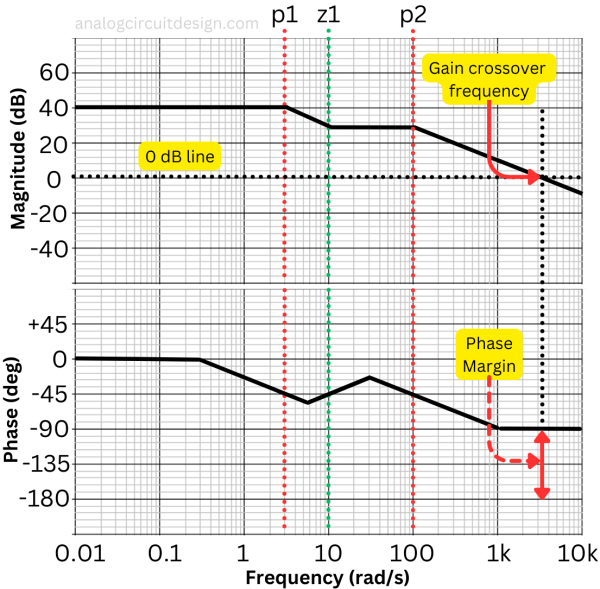
The phase never reaches -180° so the phase cross-over frequency lies at infinity. The gain at infinity is zero, which means it has an infinite gain margin.
To know how to draw a bode plot please visit this page: How to draw a bode plot?