What is SR Latch?
The SR (Set-Reset) latch is a 1-bit memory with SET and RESET inputs labelled as ‘S’ and ‘R,’ respectively. It is also a bistable device meaning it has 2 stable states namely 0 and 1. The SET input sets the device to produce output (Q) equal to 1, while the RESET input resets the device to produce output equal to 0.
| S | R | Qn+1 | Qn+1 | Note |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | FORBIDDEN |
| 0 | 1 | 1 | 0 | SET |
| 1 | 0 | 0 | 1 | RESET |
| 1 | 1 | Qn | Qn | RETAIN |
| S | R | Qn+1 | Qn+1 | Note |
|---|---|---|---|---|
| 0 | 0 | Qn | Qn | RETAIN |
| 0 | 1 | 1 | 0 | RESET |
| 1 | 0 | 0 | 1 | SET |
| 1 | 1 | 0 | 0 | FORBIDDEN |
- When both ‘S’ and ‘R’ are 0, the latch maintains its state. Whatever ‘Q’ was, it stayed the same.
- When ‘S’ is 0 and ‘R’ is 1, the latch resets, forcing ‘Q’ to be 0.
- When ‘S’ is 1 and ‘R’ is 0, the latch sets, making ‘Q’=1.
- When both ‘S’ and ‘R’ are 1, it’s an invalid or ambiguous condition (often referred to as a “forbidden” state in SR latch), resulting in both Q and Q being the same and 0.
Symbol of SR Latch
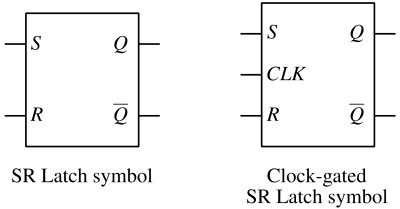
The symbol of a Gated SR latch typically used in digital circuit diagrams resembles a basic SR latch with an additional input for the gate/clock signal (CLK). The gate signal acts as a control to enable or disable the inputs S (Set) and R (Reset) from affecting the latch’s state.
Gated SR latch
Gated SR latch has a third control called CLOCK (CLK) as mentioned above. When CLK=0, the latch is in RETAIN state, not allowing any external SET or RESET signal to enter. Only when CLK=1, the inputs S and R are allowed to change the output Q.
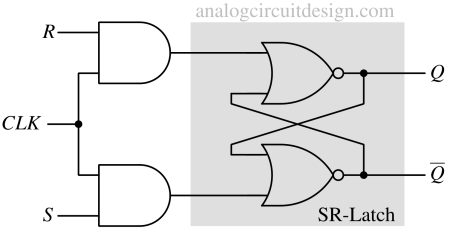
In NOR based gated S R latch, when CLK = 0, both the inputs to the internal S R latch are 0. This state according to the truth table of NOR gate S R latch is the RETAIN state.
In NAND based gated S R latch, when CLK = 0, both the inputs to the internal S R latch are 1. This state according to the truth table of NAND gate S R latch (Table 1) is the RETAIN state. In this state, external inputs are not allowed to change the internal state/data.
| Trigger | Inputs | Output | Note | ||||
|---|---|---|---|---|---|---|---|
| Present state | |||||||
| CLK | S | R | Qn+1 | ||||
| 0 | X | X | Qn | RETAIN | |||
| 1 | 0 | 0 | Qn | RETAIN | |||
| 1 | 0 | 1 | 1 | RESET | |||
| 1 | 1 | 0 | 0 | SET | |||
| 1 | 1 | 1 | 0 | FORBIDDEN | |||
In Table 3, the truth table adds CLK as another input. Table 3 is just an extension of Table 1. This shows that if CLK=0, the input S and R can be anything in a gated SR latch.
What is SR Flip-Flop?
The term “flip-flop” reflects its operation, allowing it to be “flipped” to a logic set state or “flopped” back to the opposing logic reset state.
Two SR latches (gated) are connected in cascade with inverted clock input to create an SR Flip-Flop. The truth table of the S R Flip-Flop is similar to the S R latch except the excitation is done using the rising or falling edge of the clock.
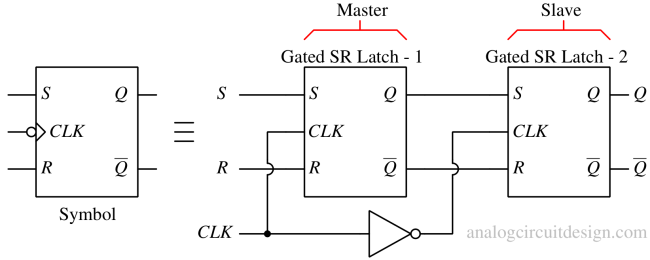
Working of a S R flip-flop
Let’s take the example of the S R flip-flop we have in Fig 4.
When CLK = 1, the latch-1 is activated while latch-2 is deactivated. This means that S and R signals can now change the state of the latch-1, however, the internal state of the latch-2 cannot be changed. If S = 1, R = 0 the output of the latch-1 is 1 (Q=1). However, it does not affect the state of the latch 2.
As soon as the CLK = 0, latch-1 deactivates and latch-2 is activated. The latch-2 captures the output of latch-1 while latch-1 RETAIN the state it had when CLK was 1. The output of latch-1 was Q=1 (and Q = 0, because S=1, R=0) so, the input to latch 2 is again S = 1 and R = 0. Hence the output of latch-2 is again Q = 1. Since the latch-1 is disabled, nothing can enter this flip-flop.
When CLK = 1 again, the latch-1 is enabled while latch-2 is disabled again. Since, the latch-2 is disabled, the latch-2’s state is unchanged while latch-1 can change its state. The output of latch-2 is the data stored in the SR flip-flop. This SR flip-flop still has the problem of the forbidden state as shown in the truth table of SR flip-flop.
Truth Table of SR Flip-Flop
| Trigger | Inputs | Output | Note | ||||
|---|---|---|---|---|---|---|---|
| Present state | |||||||
| CLK | S | R | Qn+1 | ||||
| not ↓ | X | X | Qn | RETAIN | |||
| ↓ | 0 | 0 | Qn | RETAIN | |||
| ↓ | 0 | 1 | 1 | RESET | |||
| ↓ | 1 | 0 | 0 | SET | |||
| ↓ | 1 | 1 | 0 | FORBIDDEN | |||
Excitation table of SR Flip-Flop
| Qn | Qn+1 | S | R |
|---|---|---|---|
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | X | 0 |
Forbidden state in SR Latch and SR Flip-Flop
In both NAND and NOR gate-based SR latches, there is a restriction against the undefined input condition. In the NAND gate-based SR latch, setting both SET and RESET inputs to “0” is not allowed, while in the NOR gate-based SR latch, setting both SET and RESET inputs to “1” is forbidden. This limitation represents a drawback of the SR flip-flop. The flip-flop/latch does not get damaged in forbidden state.
The forbidden state in both NAND and NOR gate-based SR latches is crucial to prevent:
- In this state, the feedback is over-ridden, and latch cannot store any data into it.
- In certain scenarios, both Q and Q outputs in a flip-flop may have the same value, contrary to the typical expectation that Q is the opposite of Q. The logic following the SR Latch may go haywire if Q and Q are same value.