Stability of control systems¶
Stability refers to the ability of a closed-loop system to maintain a state of equilibrium or to return to that state after being subjected to disturbances or changes. A stable control system is one in which the output remains bounded and does not exhibit uncontrolled or oscillatory behavior, even when subjected to external forces or variations in input. Mathematical expressions like phase margin and gain margin are used to quantify the stability of a negative feedback system.
Bounded input and Bounded output stability¶
Bounded-Input and Bounded-Output (BIBO) stability, often called input-output stability, assesses how a system responds to bounded (limited) inputs. A system is considered BIBO stable if the output remains bounded for any bounded input signal, meaning it does not grow without limit.
Categories of stability¶
A system can be categorized into 3 categories in terms of stability :
- Stable
- Marginal stable
- Unstable
Stable system¶
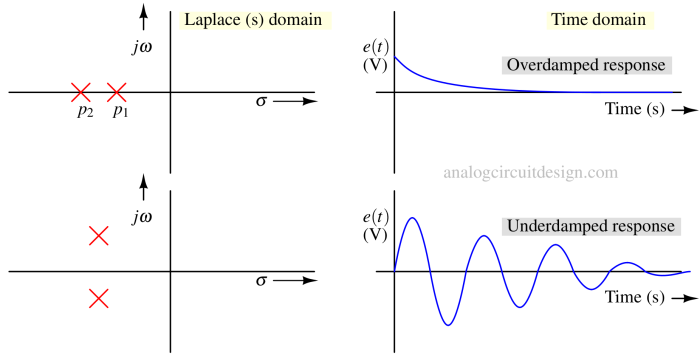
The system is considered stable if the poles of the system's transfer function are on the \left side of the s-plane. But as the poles move closer to the origin, the system's stability decreases. A pulse response (Fig 1) shows that poles lying on the real axis have an overdamped response. The transient response is sinusoidal but exponentially decaying (underdamped response) for poles in the second and third quadrants.
Dominant and non-dominant poles¶
Poles that are near the origin are called dominant poles. So, if a stable system has poles at p1 and p2 (as shown in Fig 2), p1 is considered the dominant pole of that system. p2 is considered a non-dominant pole of the system. In transient response, the contribution due to p2 will decay faster and the response will be dominated by dominant pole p1.
Types of stable systems¶
A stable system can be categorized as follows:
- Unconditionally (absolute) stable system
- Conditionally stable system
Marginal stable system¶
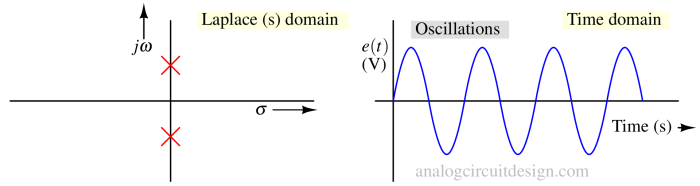
A system is marginally stable if its poles are on the imaginary axis and don't repeat. The time domain pulse response shows oscillation at a steady amplitude. The initial condition (amplitude of the input) defines the amplitude.
Unstable system¶
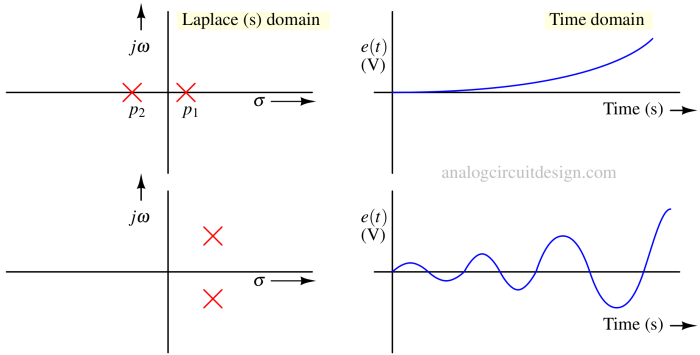
If a system has any poles on the \right side of the s-plane, it's called unstable. Even just one pole on the \right side can make the system unstable. The output grows with time. The oscillation amplitude grows exponentially with time. In real system, the amplitude will rise till the supply voltage is reached.