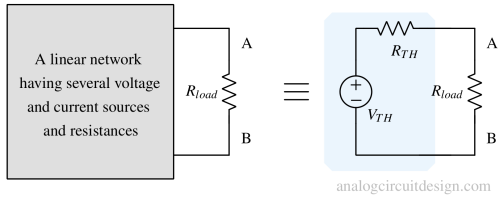
Thevenin's theorem

Thevenin's Theorem¶

Thevenin's theorem states, "Any linear electrical network containing only voltage sources, current sources, and resistances can be replaced by an equivalent combination of a voltage source VTH in a series connection with a resistance RTH." thevenin theorem concept

Step 1: Identify and differentiate load and the network¶

Rload is usually the resistor through which we want to determine the current and voltage. Apart from the Rload, every other circuit component forms the network, which needs to be simplified to Thevenin equivalent circuit.

norton theorem procedure step 1.

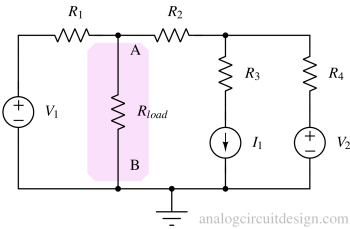
Step 2: Find the open circuit voltage at node A and B¶

thevenin_step_2-1

Using the superposition theorem,

$$V_{TH}=\cfrac{R_2+R_4}{R_1+R_2+R_4}V_1+\cfrac{R_1}{R_1+R_2+R_4}V_2+\cfrac{R_4}{R_1+R_2+R_4}I_1R_1$$

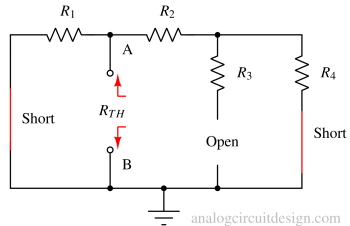
Step 3: Find the equivalent resistance¶

The equivalent RTH is the resistance the circuit between terminals A and B would have if a short circuit replaced all ideal voltage sources and an open circuit replaced all ideal current sources.

$$R_{TH}=R_1||(R_2+R_4)$$

The method of finding the resistance is identical to Norton's resistance.

thevenin_step_3-1

Step 4: Create the Thevenin network¶

Thevenin_Equivalent_Circuit-1 — Fig : Thevenin equivalent circuit

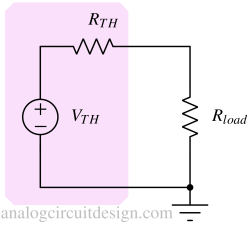
Step 5: Find the current through the load¶

The current through the load,

$$I_{load}=\cfrac{V_{TH}}{R_{load}+R_{TH}}$$

The voltage across the load,

$$V_{load}=\cfrac{V_{TH}}{R_{load}+R_{TH}}R_{load}$$