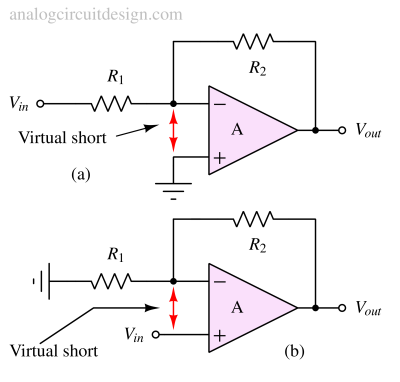
Virtual short and virtual ground in opamp¶
Any negative feedback system with significant amount of gain would attempt to minimize the voltage error at the input terminals. This means that the steady-state value of the difference between the two input terminals would be nearly zero. This similarity in two input pins in negative feedback circuits is called virtual short. It is also called virtual ground if the non-inverting terminal is tied to a ground terminal. There is no physical/electrical/magnetic connection between the two terminals.
An opamp is a negative feedback system if the [loop gain is negative]. If the opamp is in positive feedback, the virtual short concept does not hold because the error (vip - vim) will exponentially increase.
Since some portion of the output is feedback to inverting terminal of the opamp, the output will attempt to ensure that the voltage difference between the two inputs is zero (minimal).
$$v_e=\left(v_{ip}-v_{im}\right)$$
$$v_{out}=A\cdot{}v_e$$
From the above figure,
$$v_{im}=v_{out}$$
$$\implies{}v_e=\cfrac{v_{ip}}{1+A}$$
If A is a large value, ve becomes very small, so the difference between vip and vim also becomes small. Mathematically, this is virtual short.

How to find loop gain (LG)?¶
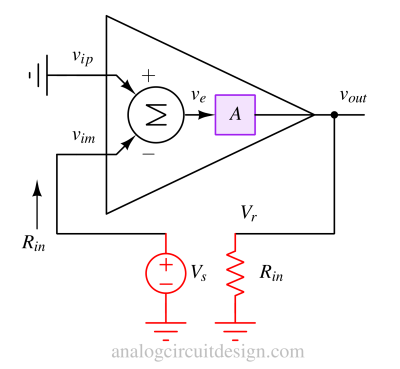
We will cut the loop between vout and vim terminals as shown in the above figure. After cutting the loop, we will insert a voltage source (Vs) at the inverting terminal of the opamp. We will also attach the input resistance (Rin) at vout terminal. Also, we will connect the non-inverting terminal (vip) to the ground so that no voltage signal comes from that terminal. That means vip is 0.
Now, let's find the transfer function from Vs to Vr . This transfer function is also called loop gain (LG).
$$v_e=(0-V_s)$$
$$V_{r}=A\cdot{}v_e$$
$$\implies{}V_r=-A\cdot{}V_s$$
$$\implies{}\cfrac{V_r}{V_s}=-A=\text{LG}$$
The sign of the loop gain (LG) is coming to be negative. Therefore the system is a negative feedback system. Intuitively, this means whatever change is being forced in the inverting terminal of the opamp is opposed by the output terminal.
What is virtual ground ?¶
The term "virtual ground" is used interchangeably with "virtual short". In the case of inverting amplifier configuration, we observe that the non-inverting terminal is connected to the ground terminal of the circuit. Using the virtual short concept, the inverting terminal is now virtually connected to the ground. That is why "virtual ground".
Importance of virtual short in negative feedback opamp¶
It allows us to analyze and design circuits using idealized assumptions, simplifying complex calculations and reducing errors. This simplification allows us to focus on the behavior of the signals at the input and output terminals, without getting bogged down in the internal workings of the op-amp.
Common misconceptions about virtual shorts¶
- One misconception is that a virtual short implies there is no voltage difference between the input terminals. While the voltage difference is indeed very small in an ideal op amp, it is not zero. The virtual short concept simply states that the voltage difference is minimized due to the op amp's feedback mechanism.
- Another misconception is that a virtual short means the input terminals are physically connected. In reality, the inputs of an op-amp are separate and isolated, but the high gain and feedback mechanism creates the illusion of a virtual connection.
- It is also important to note that the virtual short concept applies only when the opamp is in negative feedback. Real-world op amps have offsets which may add some ~mV of voltage difference. Understanding these limitations is crucial when designing practical circuits.