Source transformation¶
Source transformation is a method to simplify circuit analysis. This concept helps us to convert a complex circuit into a simpler equivalent circuit whose v-i characteristics are identical to the original circuit.
Procedure for source transformation¶
A source transformation is a process of replacing a voltage source (Vs) in series with a resistor (Rs) by a current source (Is) in parallel with a resistor (Rp) or vice-versa. In other words, source transformation involves converting a Thevenin equivalent circuit into a Norton equivalent or vice-versa. Source transformation also applies to dependent sources.
Some points to note during source transformation :
- While converting a voltage source into a current source, the arrow direction of the current source is kept towards the positive terminal of the replaced voltage source.
- Source transformation is impossible for an ideal current source (infinite output/parallel resistance) and an ideal voltage source (zero output/series resistance).
Example¶
Calculate the current through the 12k resistor in Figure 1.
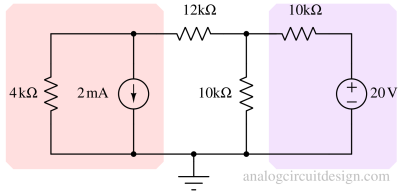
The above figure shows that the 2mA current source is forming a supermesh. So, the analysis becomes lengthy because it involves writing multiple simultaneous equations. The idea is to simplify the circuit to the po\int where we must write only one equation with only one variable.
If we convert the current source and 4kΩ resistor into a voltage source, we can combine 4kΩ and 12kΩ together, as shown in the next step. Also, we can combine 10kΩ and 10kΩ resistors.
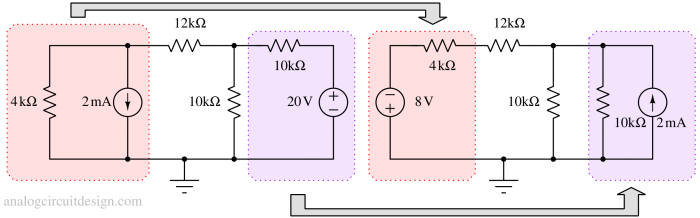
Again we have one voltage source (-8V) and one current source (2mA) as shown in Fig 3. We have 2 meshes, so we need to write 2 simultaneous equations. So, not simplified enough at this po\int.
So, we do source transformation again to get the voltage source in series with a resistor. Now, we have only one equation to solve.
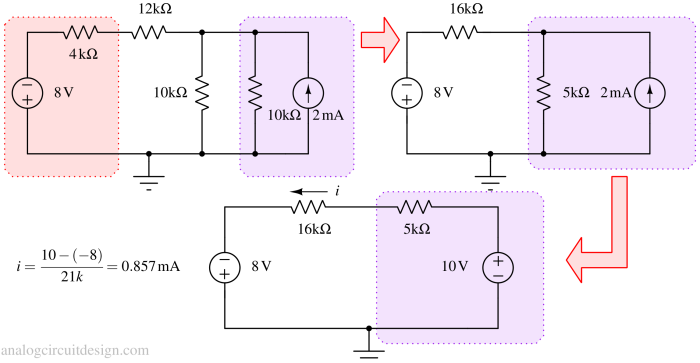
Since the current through the 16k resistor is the same as the current through the 12k resistor (because both were combined in series), therefore the current through the 12k resistor is 0.857mA, as calculated in Figure 3.